
Question Number 48129 by kaivan.ahmadi last updated on 19/Nov/18
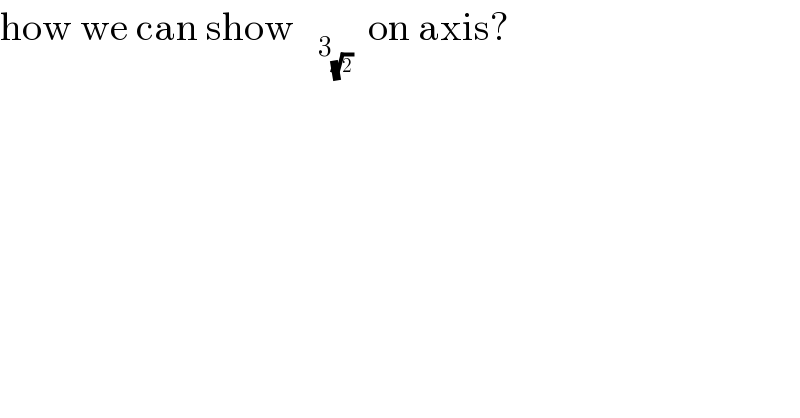
$$\mathrm{how}\:\mathrm{we}\:\mathrm{can}\:\mathrm{show}\:\:\:_{\mathrm{3}_{\sqrt{\mathrm{2}}} } \:\:\mathrm{on}\:\mathrm{axis}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Nov/18

$${trying}\:{to}\:{solve}... \\ $$$$\left.\mathrm{1}\right){first}\:{plot}\:{graph}\:{y}={x}^{\mathrm{3}} \\ $$$$\left.\mathrm{2}\right){plot}\:{point}\:{p}\left(\mathrm{0},\mathrm{2}\right)\:{on}\:{yaxis} \\ $$$$\left.\mathrm{3}\right){draw}\:{straight}\:{line}\:{y}=\mathrm{2}\:{which}\:{is}\:{parallel} \\ $$$${to}\:{x}\:{axis} \\ $$$$\left.\mathrm{4}\right){let}\:{straight}\:{line}\:{y}=\mathrm{2}\:\:{cuts}\:{curve}\:{at}\:{point}\:{q} \\ $$$$\:{the}\:{co}−{oridinate}\:{of}\:{point}\:{q}\:{is}\:\left(\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{2}\right) \\ $$$$\left.\mathrm{5}\right){draw}\:{straight}\:{line}\:{parralel}\:{to}\:{yaxis}\:{from} \\ $$$${point}\:{q} \\ $$$$\left.\mathrm{6}\right){let}\:{this}\:{straight}\:{line}\:{cuts}\:{x}\:{axis}\:{at}\:{point}\:{say} \\ $$$${M}\:\:{so}\:{co}\:{ordinate}\:{of}\:{M}\:{is}\left(\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{0}\right) \\ $$
Commented by MJS last updated on 20/Nov/18

$$\mathrm{this}\:\mathrm{works}\:\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{way}\:\mathrm{to}\:\mathrm{exactly} \\ $$$$\mathrm{construct}\:\mathrm{it} \\ $$
Commented by kaivan.ahmadi last updated on 20/Nov/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{would}\:\mathrm{you}\:\mathrm{show}\:\mathrm{it}\:\mathrm{geometricaly}? \\ $$
Commented by MJS last updated on 20/Nov/18

$$\mathrm{it}'\mathrm{s}\:\mathrm{impossible}. \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{old}\:\mathrm{problem}\:\mathrm{of}\:``\mathrm{doubling}\:\mathrm{the}\:\mathrm{cube}'' \\ $$$$\mathrm{which}\:\mathrm{has}\:\mathrm{been}\:\mathrm{proven}\:\mathrm{impossible}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{19}^{\mathrm{th}} \:\mathrm{century} \\ $$
Commented by kaivan.ahmadi last updated on 20/Nov/18
$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{ur}\:\mathrm{answer} \\ $$
Commented by MJS last updated on 21/Nov/18
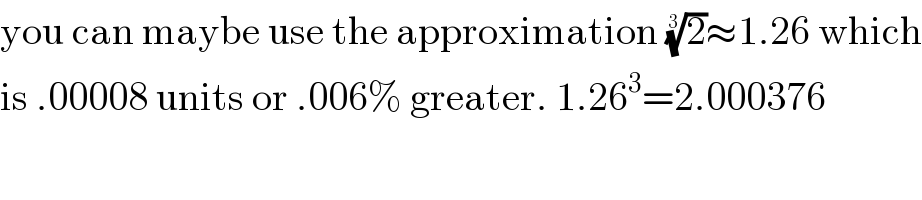
$$\mathrm{you}\:\mathrm{can}\:\mathrm{maybe}\:\mathrm{use}\:\mathrm{the}\:\mathrm{approximation}\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\approx\mathrm{1}.\mathrm{26}\:\mathrm{which} \\ $$$$\mathrm{is}\:.\mathrm{00008}\:\mathrm{units}\:\mathrm{or}\:.\mathrm{006\%}\:\mathrm{greater}.\:\mathrm{1}.\mathrm{26}^{\mathrm{3}} =\mathrm{2}.\mathrm{000376} \\ $$
