
Question Number 48078 by cesar.marval.larez@gmail.com last updated on 19/Nov/18
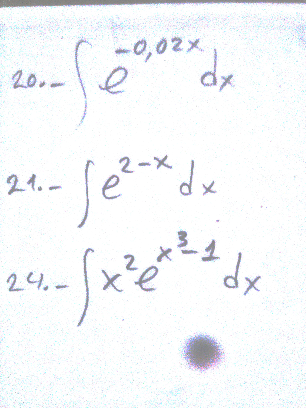
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
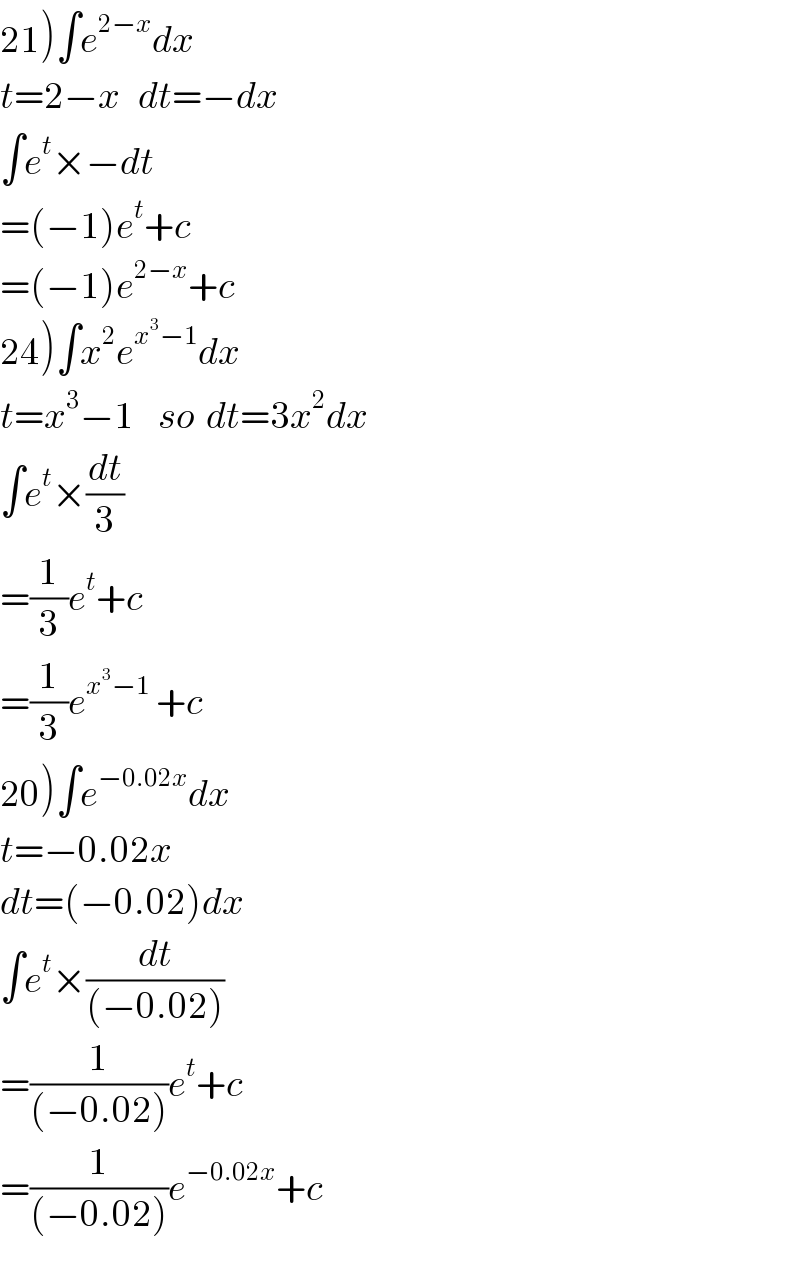
$$\left.\mathrm{21}\right)\int{e}^{\mathrm{2}−{x}} {dx} \\ $$$${t}=\mathrm{2}−{x}\:\:\:{dt}=−{dx} \\ $$$$\int{e}^{{t}} ×−{dt} \\ $$$$=\left(−\mathrm{1}\right){e}^{{t}} +{c} \\ $$$$=\left(−\mathrm{1}\right){e}^{\mathrm{2}−{x}} +{c} \\ $$$$\left.\mathrm{24}\right)\int{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{3}} −\mathrm{1}} {dx} \\ $$$${t}={x}^{\mathrm{3}} −\mathrm{1}\:\:\:\:{so}\:\:{dt}=\mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$$\int{e}^{{t}} ×\frac{{dt}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{{t}} +{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{{x}^{\mathrm{3}} −\mathrm{1}} \:+{c} \\ $$$$\left.\mathrm{20}\right)\int{e}^{−\mathrm{0}.\mathrm{02}{x}} {dx} \\ $$$${t}=−\mathrm{0}.\mathrm{02}{x}\: \\ $$$${dt}=\left(−\mathrm{0}.\mathrm{02}\right){dx} \\ $$$$\int{e}^{{t}} ×\frac{{dt}}{\left(−\mathrm{0}.\mathrm{02}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(−\mathrm{0}.\mathrm{02}\right)}{e}^{{t}} +{c} \\ $$$$=\frac{\mathrm{1}}{\left(−\mathrm{0}.\mathrm{02}\right)}{e}^{−\mathrm{0}.\mathrm{02}{x}} +{c} \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 19/Nov/18

$${Sir},\:{thank}\:{u}\: \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 19/Nov/18

$${U}\:{r}\:{an}\:{expert} \\ $$
