
Question Number 48075 by MJS last updated on 19/Nov/18
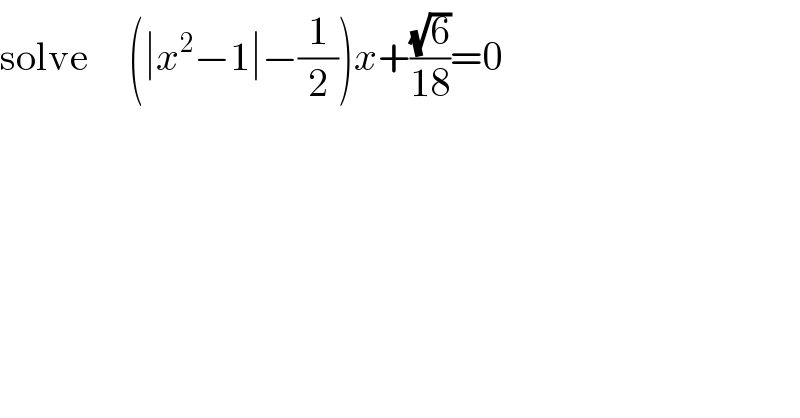
$$\mathrm{solve}\:\:\:\:\:\left(\mid{x}^{\mathrm{2}} −\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}}\right){x}+\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}=\mathrm{0} \\ $$
Commented by MJS last updated on 19/Nov/18
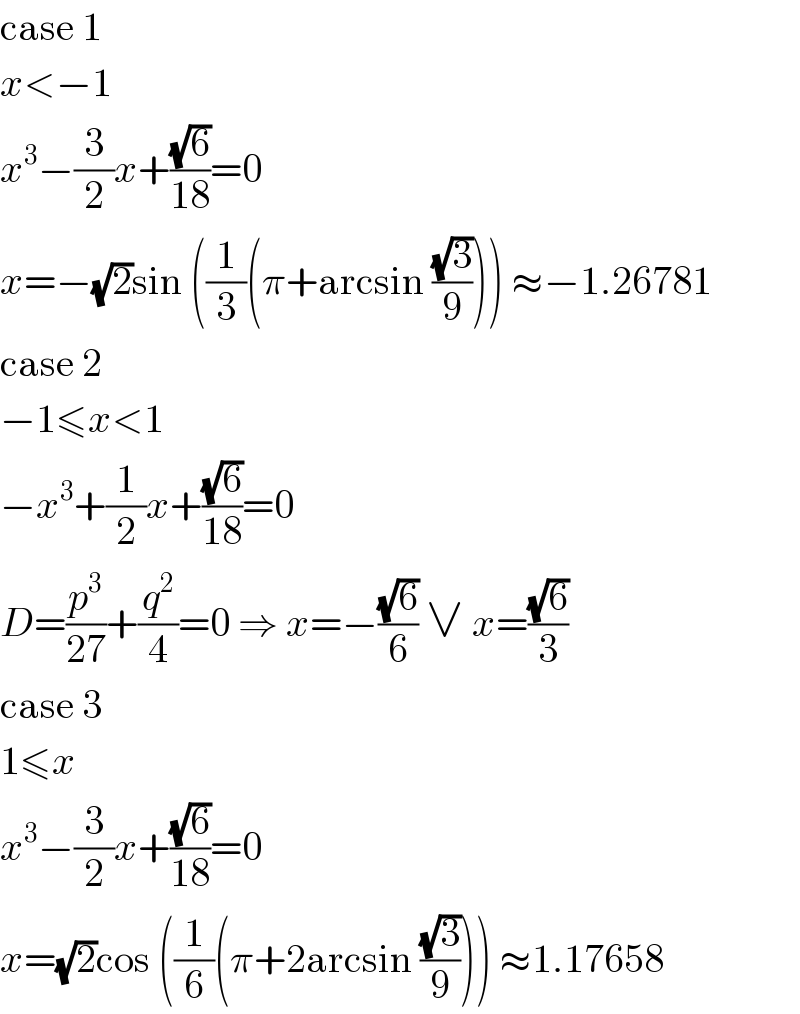
$$\mathrm{case}\:\mathrm{1} \\ $$$${x}<−\mathrm{1} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{x}+\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}=\mathrm{0} \\ $$$${x}=−\sqrt{\mathrm{2}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\right)\right)\:\approx−\mathrm{1}.\mathrm{26781} \\ $$$$\mathrm{case}\:\mathrm{2} \\ $$$$−\mathrm{1}\leqslant{x}<\mathrm{1} \\ $$$$−{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\:\vee\:{x}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\mathrm{case}\:\mathrm{3} \\ $$$$\mathrm{1}\leqslant{x} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{x}+\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}=\mathrm{0} \\ $$$${x}=\sqrt{\mathrm{2}}\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{6}}\left(\pi+\mathrm{2arcsin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\right)\right)\:\approx\mathrm{1}.\mathrm{17658} \\ $$
Answered by ajfour last updated on 19/Nov/18
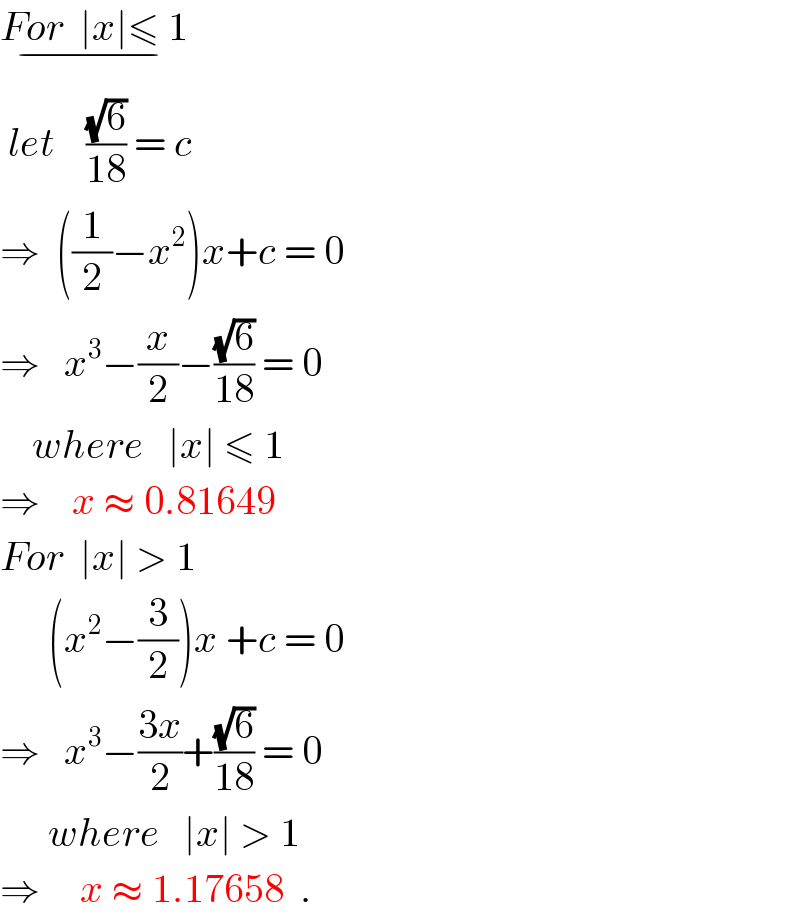
$$\underset{−} {{For}\:\:\mid{x}\mid\leqslant\:\mathrm{1}} \\ $$$$\:{let}\:\:\:\:\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}\:=\:{c} \\ $$$$\Rightarrow\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}^{\mathrm{2}} \right){x}+{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}^{\mathrm{3}} −\frac{{x}}{\mathrm{2}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}\:=\:\mathrm{0}\:\:\:\:\:\: \\ $$$$\:\:\:\:{where}\:\:\:\mid{x}\mid\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{x}\:\approx\:\mathrm{0}.\mathrm{81649} \\ $$$${For}\:\:\mid{x}\mid\:>\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\left({x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\right){x}\:+{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}^{\mathrm{3}} −\frac{\mathrm{3}{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{6}}}{\mathrm{18}}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{where}\:\:\:\mid{x}\mid\:>\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\:{x}\:\approx\:\mathrm{1}.\mathrm{17658}\:\:. \\ $$
Commented by mr W last updated on 19/Nov/18

$${please}\:{check}\:{sir}: \\ $$$${for}\:\mid{x}\mid\leqslant\mathrm{1}\:{there}\:{is}\:{another}\:{solution} \\ $$$${x}\approx−\mathrm{0}.\mathrm{4082} \\ $$$${for}\:\mid{x}\mid>\mathrm{1}\:{there}\:{is}\:{another}\:{solution} \\ $$$${x}\approx−\mathrm{1}.\mathrm{2678} \\ $$
Commented by ajfour last updated on 19/Nov/18
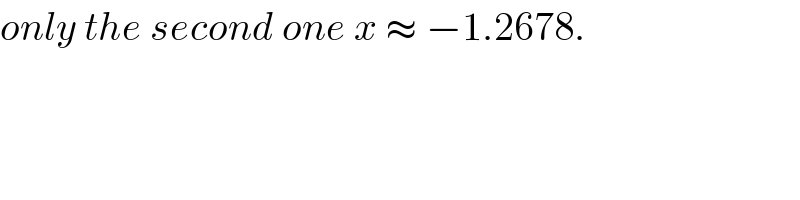
$${only}\:{the}\:{second}\:{one}\:{x}\:\approx\:−\mathrm{1}.\mathrm{2678}. \\ $$
