
Previous in Relation and Functions Next in Relation and Functions
Question Number 48068 by maxmathsup by imad last updated on 18/Nov/18
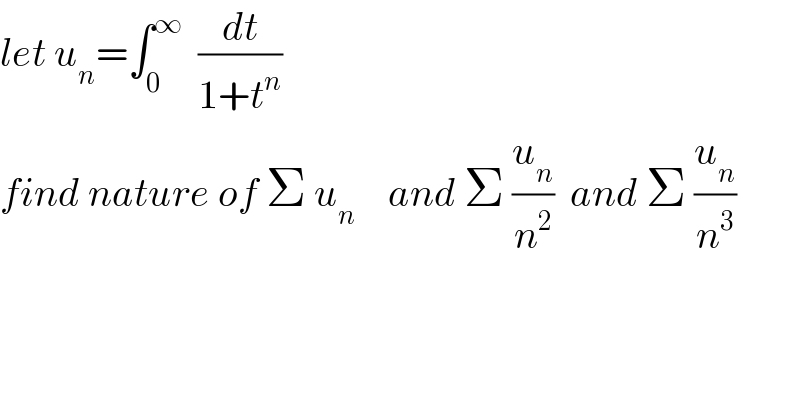
$${let}\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{{n}} } \\ $$$${find}\:{nature}\:{of}\:\Sigma\:{u}_{{n}} \:\:\:\:{and}\:\Sigma\:\frac{{u}_{{n}} }{{n}^{\mathrm{2}} }\:\:{and}\:\Sigma\:\frac{{u}_{{n}} }{{n}^{\mathrm{3}} } \\ $$
Commented by Abdo msup. last updated on 19/Nov/18
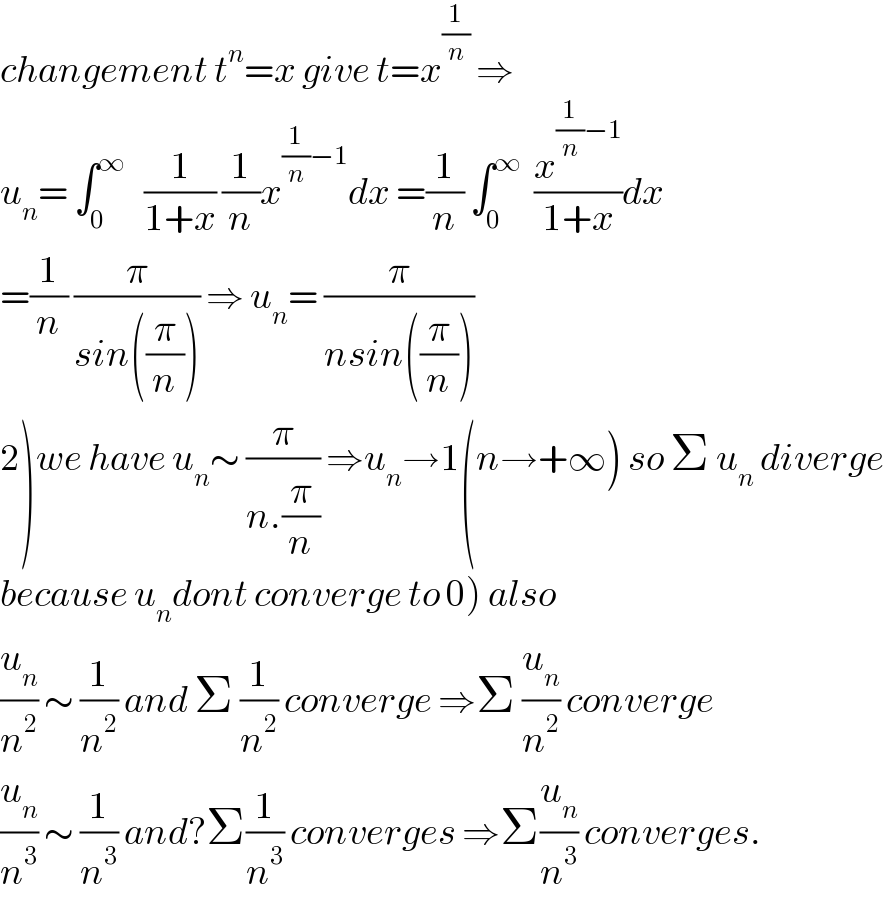
$${changement}\:{t}^{{n}} ={x}\:{give}\:{t}={x}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow \\ $$$${u}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\frac{\mathrm{1}}{{n}}{x}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dx}\:=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{1}+{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)}\:\Rightarrow\:{u}_{{n}} =\:\frac{\pi}{{nsin}\left(\frac{\pi}{{n}}\right)} \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:{u}_{{n}} \sim\:\frac{\pi}{{n}.\frac{\pi}{{n}}}\:\Rightarrow{u}_{{n}} \rightarrow\mathrm{1}\left({n}\rightarrow+\infty\right)\:{so}\:\Sigma\:{u}_{{n}} \:{diverge} \\ $$$$\left.{because}\:{u}_{{n}} {dont}\:{converge}\:{to}\:\mathrm{0}\right)\:{also} \\ $$$$\frac{{u}_{{n}} }{{n}^{\mathrm{2}} }\:\sim\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{and}\:\Sigma\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{converge}\:\Rightarrow\Sigma\:\frac{{u}_{{n}} }{{n}^{\mathrm{2}} }\:{converge} \\ $$$$\frac{{u}_{{n}} }{{n}^{\mathrm{3}} }\:\sim\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:{and}?\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:{converges}\:\Rightarrow\Sigma\frac{{u}_{{n}} }{{n}^{\mathrm{3}} }\:{converges}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18
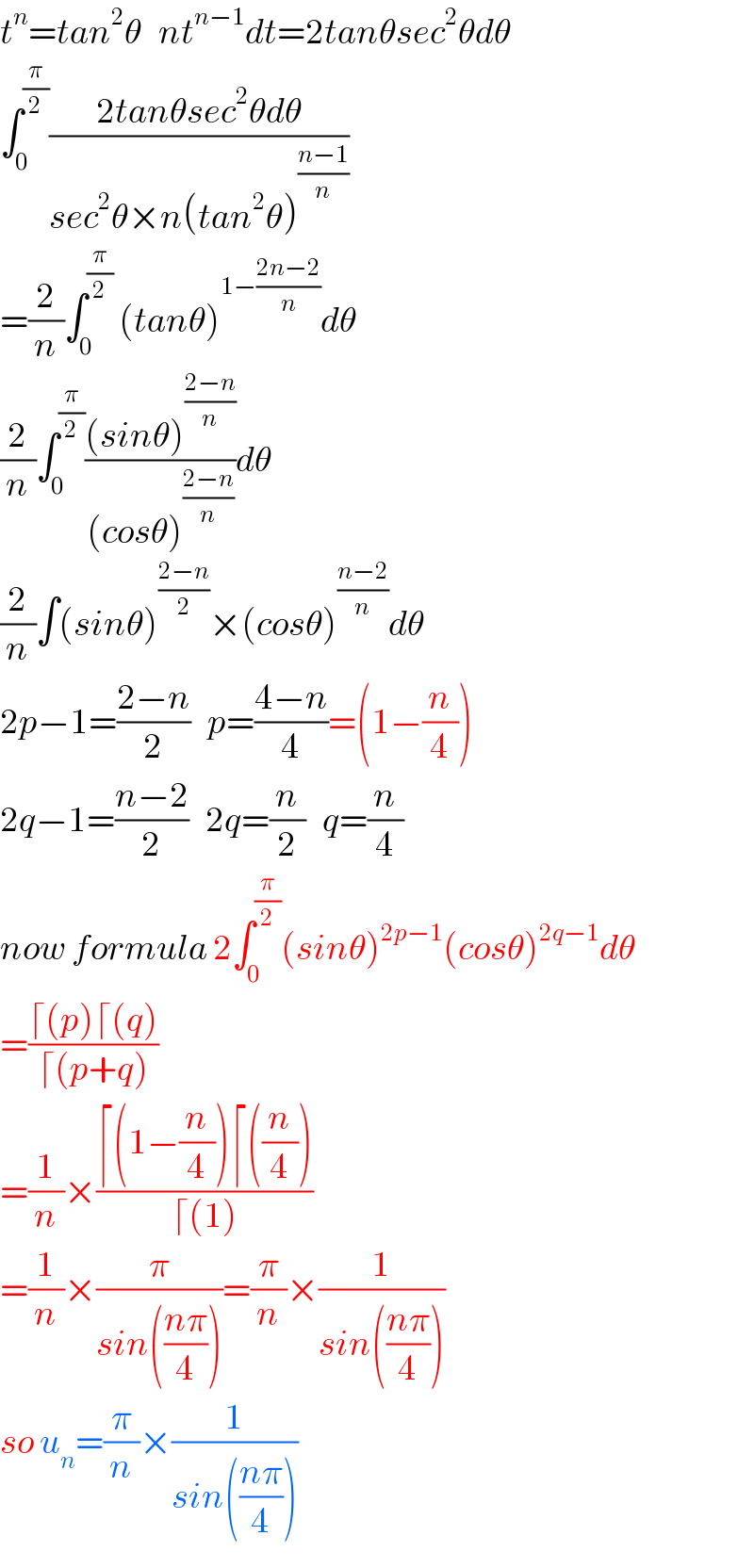
$${t}^{{n}} ={tan}^{\mathrm{2}} \theta\:\:\:{nt}^{{n}−\mathrm{1}} {dt}=\mathrm{2}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{tan}\theta{sec}^{\mathrm{2}} \theta{d}\theta}{{sec}^{\mathrm{2}} \theta×{n}\left({tan}^{\mathrm{2}} \theta\right)^{\frac{{n}−\mathrm{1}}{{n}}} } \\ $$$$=\frac{\mathrm{2}}{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left({tan}\theta\right)^{\mathrm{1}−\frac{\mathrm{2}{n}−\mathrm{2}}{{n}}} {d}\theta \\ $$$$\frac{\mathrm{2}}{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({sin}\theta\right)^{\frac{\mathrm{2}−{n}}{{n}}} }{\left({cos}\theta\right)^{\frac{\mathrm{2}−{n}}{{n}}} }{d}\theta \\ $$$$\frac{\mathrm{2}}{{n}}\int\left({sin}\theta\right)^{\frac{\mathrm{2}−{n}}{\mathrm{2}}} ×\left({cos}\theta\right)^{\frac{{n}−\mathrm{2}}{{n}}} {d}\theta \\ $$$$\mathrm{2}{p}−\mathrm{1}=\frac{\mathrm{2}−{n}}{\mathrm{2}}\:\:\:{p}=\frac{\mathrm{4}−{n}}{\mathrm{4}}=\left(\mathrm{1}−\frac{{n}}{\mathrm{4}}\right) \\ $$$$\mathrm{2}{q}−\mathrm{1}=\frac{{n}−\mathrm{2}}{\mathrm{2}}\:\:\:\mathrm{2}{q}=\frac{{n}}{\mathrm{2}}\:\:\:{q}=\frac{{n}}{\mathrm{4}} \\ $$$${now}\:{formula}\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\mathrm{2}{p}−\mathrm{1}} \left({cos}\theta\right)^{\mathrm{2}{q}−\mathrm{1}} {d}\theta \\ $$$$=\frac{\lceil\left({p}\right)\lceil\left({q}\right)}{\lceil\left({p}+{q}\right)} \\ $$$$=\frac{\mathrm{1}}{{n}}×\frac{\lceil\left(\mathrm{1}−\frac{{n}}{\mathrm{4}}\right)\lceil\left(\frac{{n}}{\mathrm{4}}\right)}{\lceil\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{n}}×\frac{\pi}{{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)}=\frac{\pi}{{n}}×\frac{\mathrm{1}}{{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)} \\ $$$${so}\:{u}_{{n}} =\frac{\pi}{{n}}×\frac{\mathrm{1}}{{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)} \\ $$
