
Question Number 48066 by rahul 19 last updated on 18/Nov/18
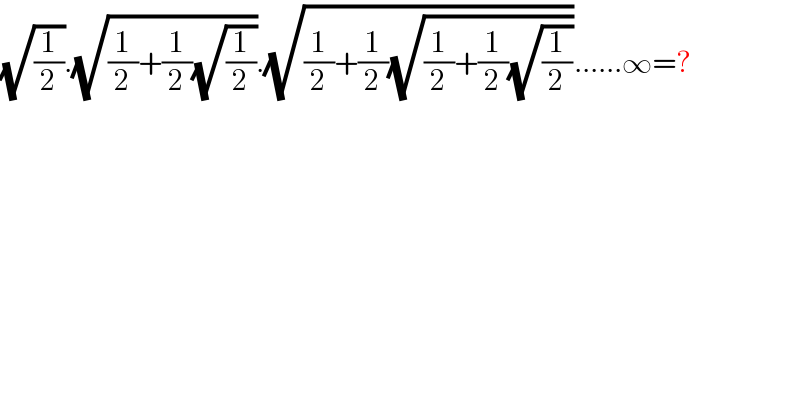
$$\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}.\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}.\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}}......\infty=? \\ $$
Commented by MJS last updated on 18/Nov/18
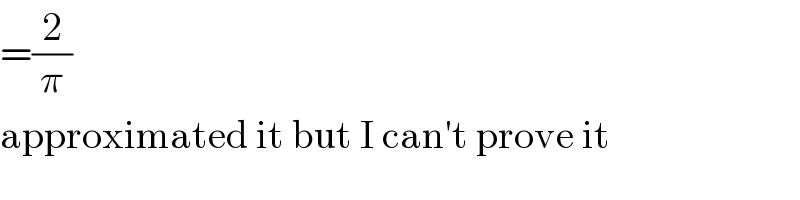
$$=\frac{\mathrm{2}}{\pi} \\ $$$$\mathrm{approximated}\:\mathrm{it}\:\mathrm{but}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{prove}\:\mathrm{it} \\ $$
Commented by maxmathsup by imad last updated on 19/Nov/18

$${we}\:{have}\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}={cos}\left(\frac{\pi}{\mathrm{4}}\right)\:,\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}=\sqrt{\frac{\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}}}={cos}\left(\frac{\pi}{\mathrm{8}}\right)\:... \\ $$$${S}_{{n}} ={cos}\left(\frac{\pi}{\mathrm{4}}\right){cos}\left(\frac{\pi}{\mathrm{8}}\right).{cos}\left(\frac{\pi}{\mathrm{16}}\right)...{cos}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)=\prod_{{k}=\mathrm{2}} ^{{n}} \:{cos}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right) \\ $$$${W}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right)\:\Rightarrow{S}_{{n}} .{W}_{{n}} =\prod_{{k}=\mathrm{2}} ^{{n}} {cos}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right){sin}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\prod_{{k}=\mathrm{2}} ^{{n}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{k}−\mathrm{1}} }\right)=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\prod_{{k}=\mathrm{2}} ^{{n}} \:\:\prod_{{k}=\mathrm{2}} ^{{n}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{k}−\mathrm{1}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\prod_{{k}=\mathrm{2}} ^{{n}} \:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right)\:\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\prod_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\prod_{{k}=\mathrm{2}} ^{{n}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{k}} }\right)}{{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}\:=\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\:.{W}_{{n}} \:\Rightarrow \\ $$$$ \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\:=\frac{\mathrm{2}}{\mathrm{2}^{{n}} \:{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\:\sim\:\frac{\mathrm{2}}{\mathrm{2}^{{n}} .\frac{\pi}{\mathrm{2}^{{n}} }}\:\left({n}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =\frac{\mathrm{2}}{\pi}\:. \\ $$
Commented by rahul 19 last updated on 20/Nov/18
thank you prof Abdo����
Commented by Abdo msup. last updated on 20/Nov/18
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by arcana last updated on 19/Nov/18
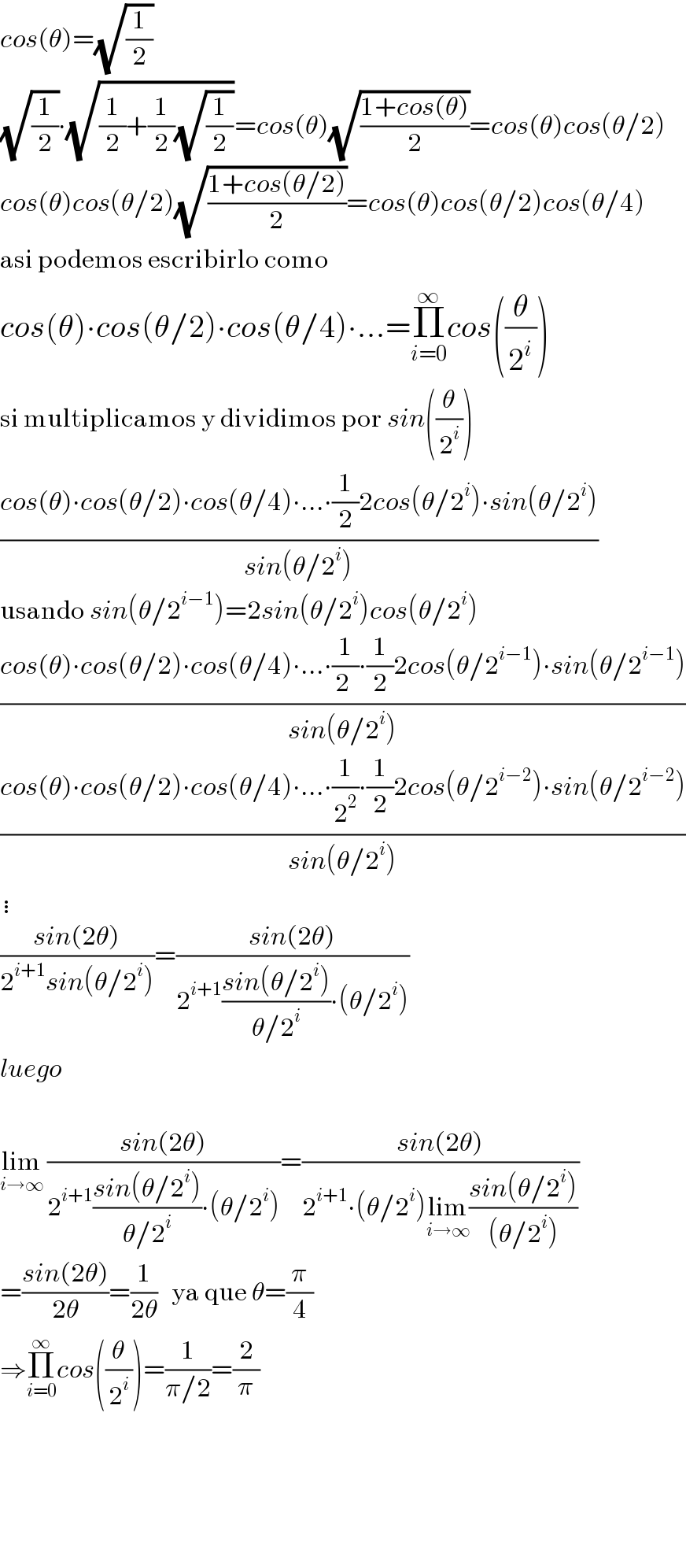
$${cos}\left(\theta\right)=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\centerdot\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}={cos}\left(\theta\right)\sqrt{\frac{\mathrm{1}+{cos}\left(\theta\right)}{\mathrm{2}}}={cos}\left(\theta\right){cos}\left(\theta/\mathrm{2}\right) \\ $$$${cos}\left(\theta\right){cos}\left(\theta/\mathrm{2}\right)\sqrt{\frac{\mathrm{1}+{cos}\left(\theta/\mathrm{2}\right)}{\mathrm{2}}}={cos}\left(\theta\right){cos}\left(\theta/\mathrm{2}\right){cos}\left(\theta/\mathrm{4}\right) \\ $$$$\mathrm{asi}\:\mathrm{podemos}\:\mathrm{escribirlo}\:\mathrm{como} \\ $$$${cos}\left(\theta\right)\centerdot{cos}\left(\theta/\mathrm{2}\right)\centerdot{cos}\left(\theta/\mathrm{4}\right)\centerdot...=\underset{{i}=\mathrm{0}} {\overset{\infty} {\prod}}{cos}\left(\frac{\theta}{\mathrm{2}^{{i}} }\right) \\ $$$$\mathrm{si}\:\mathrm{multiplicamos}\:\mathrm{y}\:\mathrm{dividimos}\:\mathrm{por}\:{sin}\left(\frac{\theta}{\mathrm{2}^{{i}} }\right) \\ $$$$\frac{{cos}\left(\theta\right)\centerdot{cos}\left(\theta/\mathrm{2}\right)\centerdot{cos}\left(\theta/\mathrm{4}\right)\centerdot...\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{cos}\left(\theta/\mathrm{2}^{{i}} \right)\centerdot{sin}\left(\theta/\mathrm{2}^{{i}} \right)}{{sin}\left(\theta/\mathrm{2}^{{i}} \right)} \\ $$$$\mathrm{usando}\:{sin}\left(\theta/\mathrm{2}^{{i}−\mathrm{1}} \right)=\mathrm{2}{sin}\left(\theta/\mathrm{2}^{{i}} \right){cos}\left(\theta/\mathrm{2}^{{i}} \right) \\ $$$$\frac{{cos}\left(\theta\right)\centerdot{cos}\left(\theta/\mathrm{2}\right)\centerdot{cos}\left(\theta/\mathrm{4}\right)\centerdot...\centerdot\frac{\mathrm{1}}{\mathrm{2}\:}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{cos}\left(\theta/\mathrm{2}^{{i}−\mathrm{1}} \right)\centerdot{sin}\left(\theta/\mathrm{2}^{{i}−\mathrm{1}} \right)}{{sin}\left(\theta/\mathrm{2}^{{i}} \right)} \\ $$$$\frac{{cos}\left(\theta\right)\centerdot{cos}\left(\theta/\mathrm{2}\right)\centerdot{cos}\left(\theta/\mathrm{4}\right)\centerdot...\centerdot\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{cos}\left(\theta/\mathrm{2}^{{i}−\mathrm{2}} \right)\centerdot{sin}\left(\theta/\mathrm{2}^{{i}−\mathrm{2}} \right)}{{sin}\left(\theta/\mathrm{2}^{{i}} \right)} \\ $$$$\vdots \\ $$$$\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}^{{i}+\mathrm{1}} {sin}\left(\theta/\mathrm{2}^{{i}} \right)}=\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}^{{i}+\mathrm{1}} \frac{{sin}\left(\theta/\mathrm{2}^{{i}} \right)}{\theta/\mathrm{2}^{{i}} }\centerdot\left(\theta/\mathrm{2}^{{i}} \right)} \\ $$$${luego} \\ $$$$ \\ $$$$\underset{{i}\rightarrow\infty} {\mathrm{lim}}\:\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}^{{i}+\mathrm{1}} \frac{{sin}\left(\theta/\mathrm{2}^{{i}} \right)}{\theta/\mathrm{2}^{{i}} }\centerdot\left(\theta/\mathrm{2}^{{i}} \right)}=\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}^{{i}+\mathrm{1}} \centerdot\left(\theta/\mathrm{2}^{{i}} \right)\underset{{i}\rightarrow\infty} {\mathrm{lim}}\frac{{sin}\left(\theta/\mathrm{2}^{{i}} \right)}{\left(\theta/\mathrm{2}^{{i}} \right)}} \\ $$$$=\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{2}\theta}=\frac{\mathrm{1}}{\mathrm{2}\theta}\:\:\:\mathrm{ya}\:\mathrm{que}\:\theta=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\underset{{i}=\mathrm{0}} {\overset{\infty} {\prod}}{cos}\left(\frac{\theta}{\mathrm{2}^{{i}} }\right)=\frac{\mathrm{1}}{\pi/\mathrm{2}}=\frac{\mathrm{2}}{\pi} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by rahul 19 last updated on 19/Nov/18
thank you so much Arcana ,����
Commented by ajfour last updated on 19/Nov/18

$${superb}! \\ $$
