
Question Number 48055 by F_Nongue last updated on 21/Nov/18
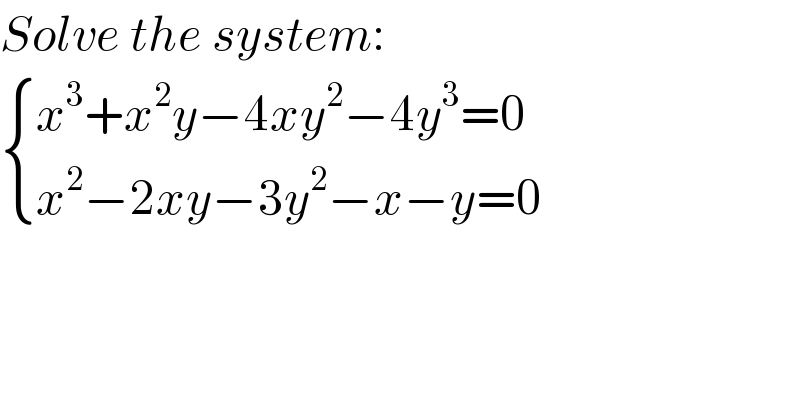
$${Solve}\:{the}\:{system}: \\ $$$$\begin{cases}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} {y}−\mathrm{4}{xy}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{3}} =\mathrm{0}}\\{{x}^{\mathrm{2}} −\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} −{x}−{y}=\mathrm{0}}\end{cases} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

$${x}=\mathrm{0}\:\:\:{y}=\mathrm{0}\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

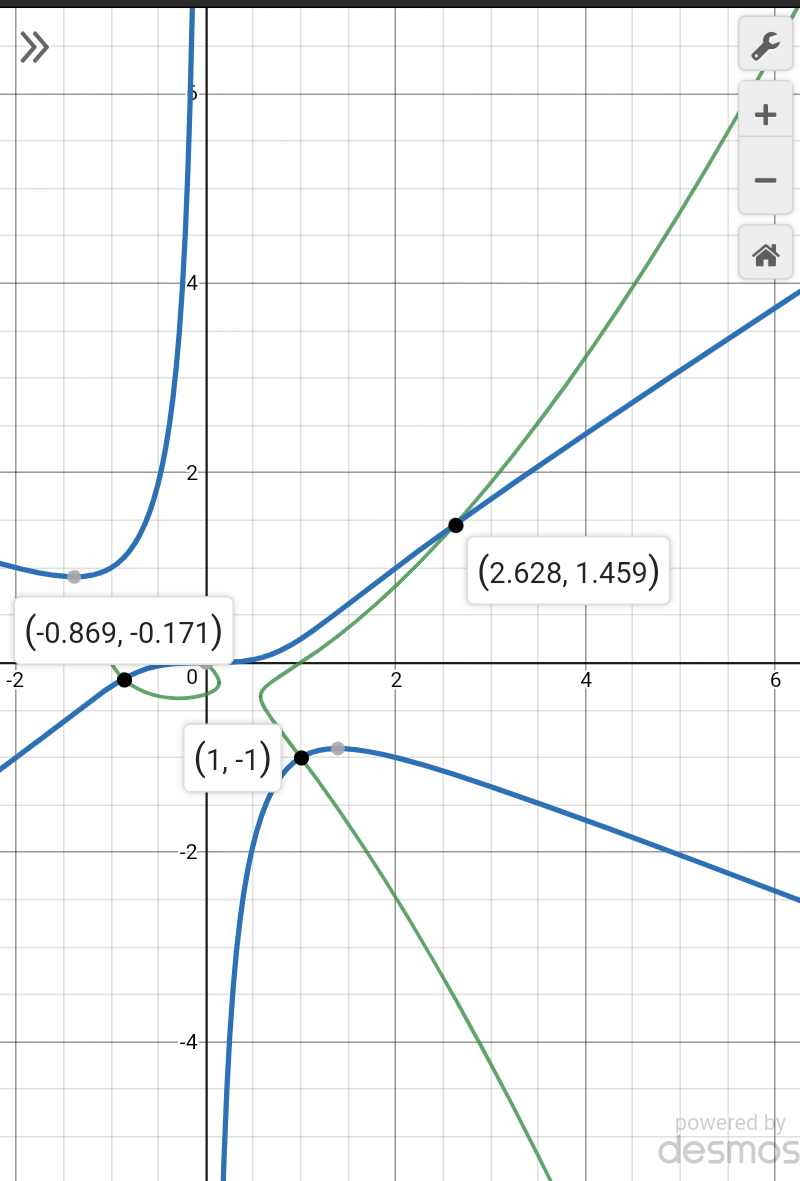
$$\left({x},{y}\right)=\left(−\mathrm{0}.\mathrm{869},−\mathrm{0}.\mathrm{171}\right) \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},−\mathrm{1}\right) \\ $$$$\left({x},{y}\right)=\left(\mathrm{2}.\mathrm{628},\mathrm{1}.\mathrm{459}\right)\:\:{obtained}\:{from}\:{graph}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
Commented by F_Nongue last updated on 19/Nov/18
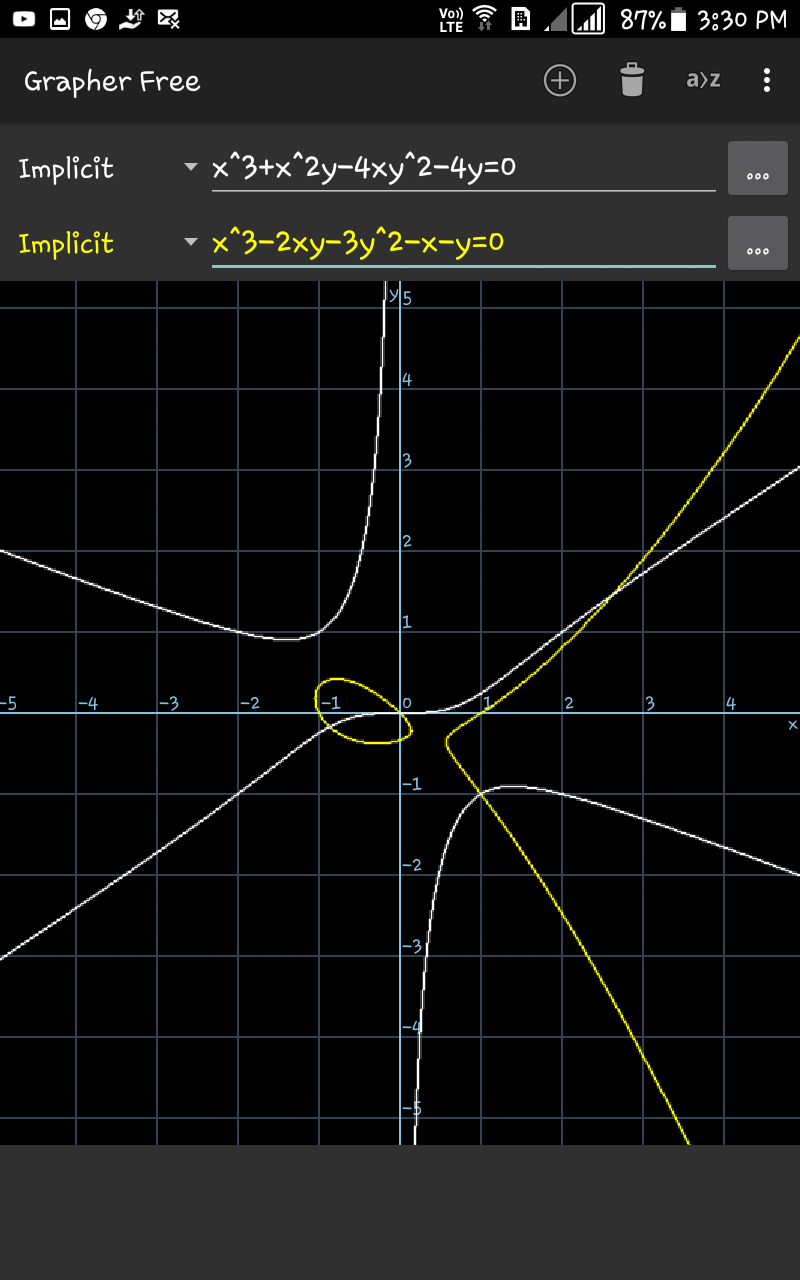
excuse me people, it was missing some power. Now it is correct
Commented by F_Nongue last updated on 19/Nov/18
I get x= 1/4 , y=-1/4
Answered by ajfour last updated on 21/Nov/18
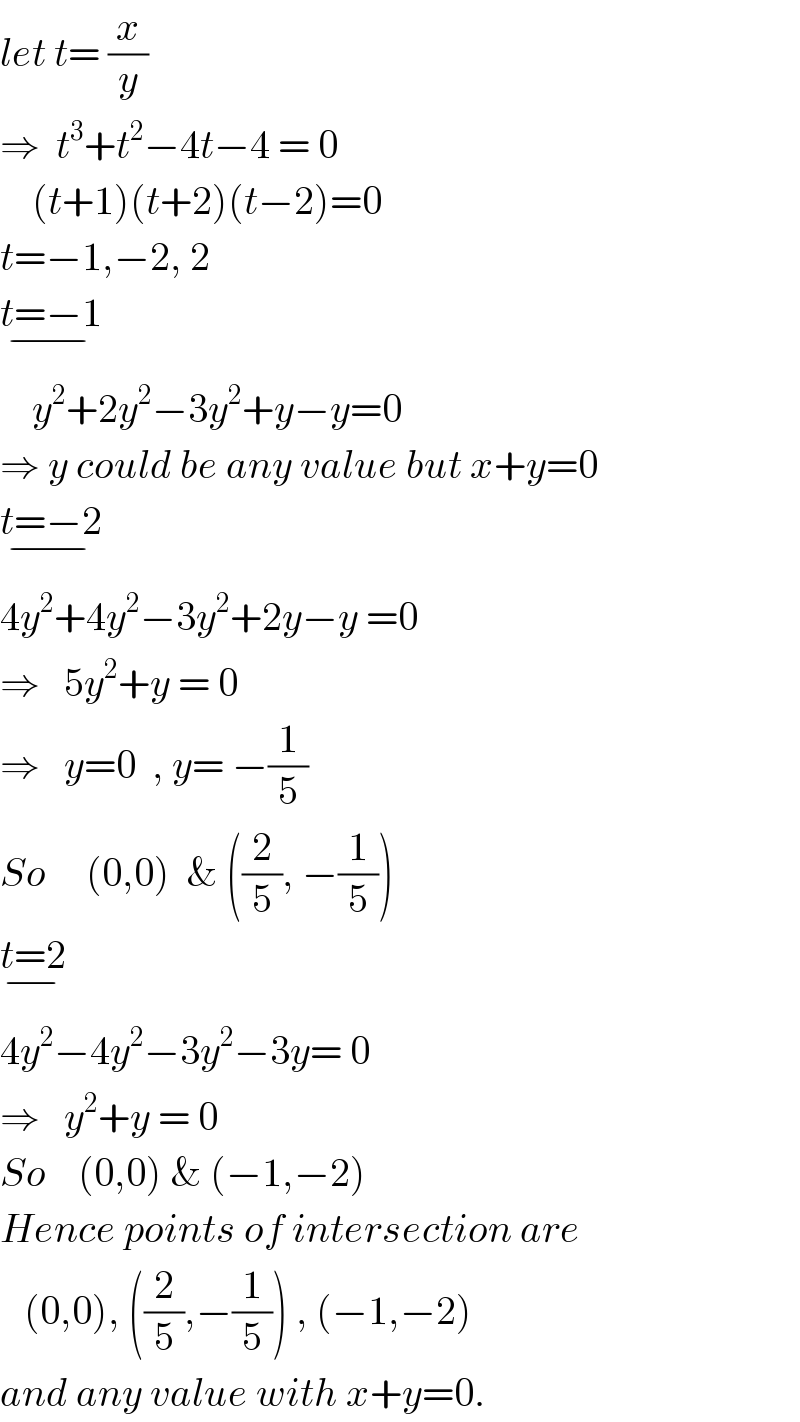
$${let}\:{t}=\:\frac{{x}}{{y}} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{4}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)\left({t}−\mathrm{2}\right)=\mathrm{0} \\ $$$${t}=−\mathrm{1},−\mathrm{2},\:\mathrm{2} \\ $$$$\underset{−} {{t}=−\mathrm{1}} \\ $$$$\:\:\:\:{y}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} +{y}−{y}=\mathrm{0} \\ $$$$\Rightarrow\:{y}\:{could}\:{be}\:{any}\:{value}\:{but}\:{x}+{y}=\mathrm{0} \\ $$$$\underset{−} {{t}=−\mathrm{2}} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} +\mathrm{2}{y}−{y}\:=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{5}{y}^{\mathrm{2}} +{y}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{y}=\mathrm{0}\:\:,\:{y}=\:−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${So}\:\:\:\:\:\left(\mathrm{0},\mathrm{0}\right)\:\:\&\:\left(\frac{\mathrm{2}}{\mathrm{5}},\:−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\underset{−} {{t}=\mathrm{2}} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{y}^{\mathrm{2}} +{y}\:=\:\mathrm{0} \\ $$$${So}\:\:\:\:\left(\mathrm{0},\mathrm{0}\right)\:\&\:\left(−\mathrm{1},−\mathrm{2}\right) \\ $$$${Hence}\:{points}\:{of}\:{intersection}\:{are} \\ $$$$\:\:\:\left(\mathrm{0},\mathrm{0}\right),\:\left(\frac{\mathrm{2}}{\mathrm{5}},−\frac{\mathrm{1}}{\mathrm{5}}\right)\:,\:\left(−\mathrm{1},−\mathrm{2}\right) \\ $$$${and}\:{any}\:{value}\:{with}\:{x}+{y}=\mathrm{0}. \\ $$
Answered by Riya Chauhan last updated on 21/Nov/18

