
Question Number 48052 by ajfour last updated on 18/Nov/18
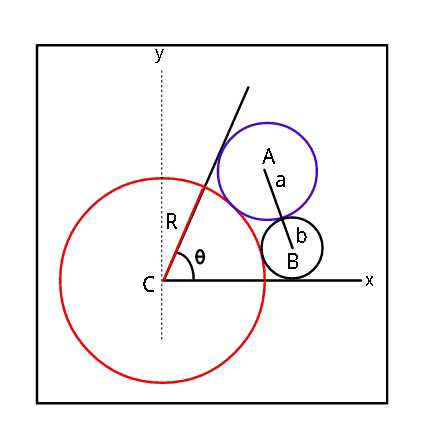
Commented by ajfour last updated on 18/Nov/18

$${Relate}\:{a},{b},{R},\theta\:. \\ $$
Answered by mr W last updated on 19/Nov/18
![(a+b)^2 =(a+R)^2 +(b+R)^2 −2(a+R)(b+R) cos (θ−sin^(−1) (a/(a+R))−sin^(−1) (b/(b+R))) a^2 +b^2 +2ab=a^2 +R^2 +2aR+b^2 +R^2 +2bR−2(a+R)(b+R) cos (θ−sin^(−1) (a/(a+R))−sin^(−1) (b/(b+R))) R^2 +(a+b)R−ab=(a+R)(b+R) cos (θ−sin^(−1) (a/(a+R))−sin^(−1) (b/(b+R))) ⇒θ=cos^(−1) ((R^2 +(a+b)R−ab)/((a+R)(b+R)))+sin^(−1) (a/(a+R))+sin^(−1) (b/(b+R)) or ((R^2 +(a+b)R−ab)/((a+R)(b+R)))=cos θ cos (sin^(−1) (a/(a+R))+sin^(−1) (b/(b+R)))+sin θ sin (sin^(−1) (a/(a+R))+sin^(−1) (b/(b+R))) ((R^2 +(a+b)R−ab)/((a+R)(b+R)))=cos θ [((R(√((2a+R)(2b+R)))−ab)/((a+R)(b+R)))]+sin θ [((a(√(R(2b+R)))+b(√(R(2a+R))))/((a+R)(b+R)))] ⇒R^2 +(a+b)R−ab=[R(√((2a+R)(2b+R)))−ab]cos θ+[a(√(R(2b+R)))+b(√(R(2a+R)))]sin θ](Q48056.png)
$$\left({a}+{b}\right)^{\mathrm{2}} =\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{R}\right)^{\mathrm{2}} −\mathrm{2}\left({a}+{R}\right)\left({b}+{R}\right)\:\mathrm{cos}\:\left(\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}−\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}={a}^{\mathrm{2}} +{R}^{\mathrm{2}} +\mathrm{2}{aR}+{b}^{\mathrm{2}} +{R}^{\mathrm{2}} +\mathrm{2}{bR}−\mathrm{2}\left({a}+{R}\right)\left({b}+{R}\right)\:\mathrm{cos}\:\left(\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}−\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}}\right) \\ $$$${R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}=\left({a}+{R}\right)\left({b}+{R}\right)\:\mathrm{cos}\:\left(\theta−\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}−\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}}\right) \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}}{\left({a}+{R}\right)\left({b}+{R}\right)}+\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}} \\ $$$${or} \\ $$$$\frac{{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}}{\left({a}+{R}\right)\left({b}+{R}\right)}=\mathrm{cos}\:\theta\:\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}}\right)+\mathrm{sin}\:\theta\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{a}+{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{{b}+{R}}\right) \\ $$$$\frac{{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}}{\left({a}+{R}\right)\left({b}+{R}\right)}=\mathrm{cos}\:\theta\:\left[\frac{{R}\sqrt{\left(\mathrm{2}{a}+{R}\right)\left(\mathrm{2}{b}+{R}\right)}−{ab}}{\left({a}+{R}\right)\left({b}+{R}\right)}\right]+\mathrm{sin}\:\theta\:\left[\frac{{a}\sqrt{{R}\left(\mathrm{2}{b}+{R}\right)}+{b}\sqrt{{R}\left(\mathrm{2}{a}+{R}\right)}}{\left({a}+{R}\right)\left({b}+{R}\right)}\right] \\ $$$$\Rightarrow{R}^{\mathrm{2}} +\left({a}+{b}\right){R}−{ab}=\left[{R}\sqrt{\left(\mathrm{2}{a}+{R}\right)\left(\mathrm{2}{b}+{R}\right)}−{ab}\right]\mathrm{cos}\:\theta+\left[{a}\sqrt{{R}\left(\mathrm{2}{b}+{R}\right)}+{b}\sqrt{{R}\left(\mathrm{2}{a}+{R}\right)}\right]\mathrm{sin}\:\theta \\ $$
Commented by ajfour last updated on 18/Nov/18

$${Thanks}\:{Sir}. \\ $$
Answered by ajfour last updated on 18/Nov/18
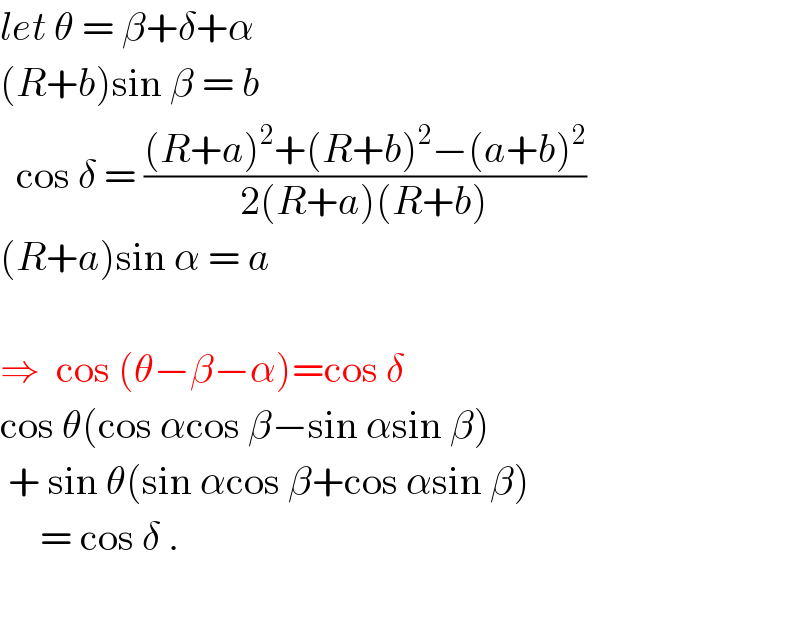
$${let}\:\theta\:=\:\beta+\delta+\alpha \\ $$$$\left({R}+{b}\right)\mathrm{sin}\:\beta\:=\:{b} \\ $$$$\:\:\mathrm{cos}\:\delta\:=\:\frac{\left({R}+{a}\right)^{\mathrm{2}} +\left({R}+{b}\right)^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}+{a}\right)\left({R}+{b}\right)} \\ $$$$\left({R}+{a}\right)\mathrm{sin}\:\alpha\:=\:{a} \\ $$$$ \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\left(\theta−\beta−\alpha\right)=\mathrm{cos}\:\delta \\ $$$$\mathrm{cos}\:\theta\left(\mathrm{cos}\:\alpha\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\mathrm{sin}\:\beta\right) \\ $$$$\:+\:\mathrm{sin}\:\theta\left(\mathrm{sin}\:\alpha\mathrm{cos}\:\beta+\mathrm{cos}\:\alpha\mathrm{sin}\:\beta\right) \\ $$$$\:\:\:\:\:=\:\mathrm{cos}\:\delta\:. \\ $$$$ \\ $$
