
Question Number 47850 by maxmathsup by imad last updated on 15/Nov/18
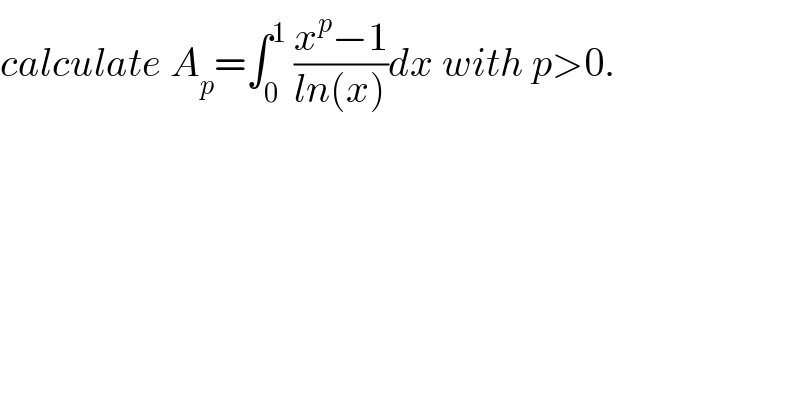
$${calculate}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{p}} −\mathrm{1}}{{ln}\left({x}\right)}{dx}\:{with}\:{p}>\mathrm{0}. \\ $$
Commented bytanmay.chaudhury50@gmail.com last updated on 16/Nov/18

$${i}\:{have}\:{tried}\:{following}\:{way} \\ $$ $${A}_{{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} −\mathrm{1}}{{lnx}}{dx} \\ $$ $$\frac{{dA}_{{p}} }{{dp}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{p}}\left(\frac{{x}^{{p}} −\mathrm{1}}{{lnx}}\right){dx} \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} {lnx}}{{lnx}}{dx} \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{p}} {dx} \\ $$ $$=\mid\frac{{x}^{{p}+\mathrm{1}} }{{p}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{p}+\mathrm{1}} \\ $$ $${dA}_{{p}} =\frac{{dp}}{{p}+\mathrm{1}} \\ $$ $$\int{dA}_{{p}} =\int\frac{{dp}}{{p}+\mathrm{1}} \\ $$ $${A}_{{p}} ={ln}\left({p}+\mathrm{1}\right)+{c} \\ $$ $${now}\:{in}\:{question}\:{p}>\mathrm{0} \\ $$ $${so}\:{here}\:{i}\:{stopped}\:{further}... \\ $$ $${but}\:{if}\:{p}=\mathrm{0}\:{assumed} \\ $$ $${then}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} −\mathrm{1}}{{lnx}}{dx} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{0}} −\mathrm{1}}{{lnx}}{dx}=\mathrm{0}={A}_{{p}=\mathrm{0}} \\ $$ $${then}\: \\ $$ $${A}_{{p}} ={ln}\left({p}+\mathrm{1}\right)+{c} \\ $$ $${A}_{{p}=\mathrm{0}} ={ln}\left(\mathrm{0}+\mathrm{1}\right)+{c} \\ $$ $$\mathrm{0}=\mathrm{0}+{c} \\ $$ $${c}=\mathrm{0} \\ $$ $${A}_{{p}} ={ln}\left({p}+\mathrm{1}\right) \\ $$ $${so}\:{A}_{{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} −\mathrm{1}}{{lnx}}{dx}={ln}\left({p}+\mathrm{1}\right) \\ $$ $${pls}\:{check}\:{sir}... \\ $$ $$ \\ $$
Commented bymaxmathsup by imad last updated on 17/Nov/18
![changement ln(x)=−t give A_p =−∫_0 ^∞ ((e^(−pt) −1)/(−t)) (−e^(−t) )dt =−∫_0 ^∞ ((e^(−(p+1)t) −e^(−t) )/t) dt =∫_0 ^∞ ((e^(−t) −e^(−(p+1)t) )/t)dt let f(p) =∫_0 ^∞ ((e^(−t) −e^(−(p+1)t) )/t) dt ⇒f^′ (p) = ∫_0 ^∞ (∂/∂p)(((e^(−t) −e^(−t) e^(−pt) )/t))dt =∫_0 ^∞ ((−e^(−t) (−t)e^(−pt) )/t)dt = ∫_0 ^∞ e^(−(p+1)t) dt =[−(1/(p+1)) e^(−(p+1)t) ]_(t=0) ^∞ =(1/(p+1)) ⇒f(p) =ln(p+1) +λ but λ =lim_(x→0) (f(p)−ln(p+1))=0 ⇒ A_p =f(p) =ln(p+1) ★ ∫_0 ^1 ((x^p −1)/(ln(x)))dx=ln(p+1) ★ with p>0.](Q47982.png)
$${changement}\:{ln}\left({x}\right)=−{t}\:{give}\:{A}_{{p}} =−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{pt}} \:−\mathrm{1}}{−{t}}\:\left(−{e}^{−{t}} \right){dt} \\ $$ $$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left({p}+\mathrm{1}\right){t}} \:−{e}^{−{t}} }{{t}}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{t}} \:−{e}^{−\left({p}+\mathrm{1}\right){t}} }{{t}}{dt}\:{let}\: \\ $$ $${f}\left({p}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} \:−{e}^{−\left({p}+\mathrm{1}\right){t}} }{{t}}\:{dt}\:\Rightarrow{f}^{'} \left({p}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\partial}{\partial{p}}\left(\frac{{e}^{−{t}} \:−{e}^{−{t}} \:{e}^{−{pt}} }{{t}}\right){dt} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \:\frac{−{e}^{−{t}} \left(−{t}\right){e}^{−{pt}} }{{t}}{dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({p}+\mathrm{1}\right){t}} {dt}\:=\left[−\frac{\mathrm{1}}{{p}+\mathrm{1}}\:{e}^{−\left({p}+\mathrm{1}\right){t}} \right]_{{t}=\mathrm{0}} ^{\infty} \\ $$ $$=\frac{\mathrm{1}}{{p}+\mathrm{1}}\:\Rightarrow{f}\left({p}\right)\:={ln}\left({p}+\mathrm{1}\right)\:+\lambda\:\:\:{but}\:\lambda\:={lim}_{{x}\rightarrow\mathrm{0}} \left({f}\left({p}\right)−{ln}\left({p}+\mathrm{1}\right)\right)=\mathrm{0}\:\Rightarrow \\ $$ $${A}_{{p}} ={f}\left({p}\right)\:={ln}\left({p}+\mathrm{1}\right) \\ $$ $$\bigstar\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{p}} −\mathrm{1}}{{ln}\left({x}\right)}{dx}={ln}\left({p}+\mathrm{1}\right)\:\bigstar\:{with}\:{p}>\mathrm{0}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Nov/18
![we know ∫_0 ^1 x^k dx=∣(x^(k+1) /(k+1))∣_0 ^1 =(1/(k+1)) now intregate both side w.r.t k in the interval say q to p ∫_q ^p dk[∫_0 ^1 x^k dx]=∫_q ^p (dk/(1+k)) taking help from advanced level intregation ∫_0 ^1 dx∫_q ^p x^k dk=∣ln(1+k)∣_q ^p ∫_0 ^1 dx[∣(x^k /(lnx))∣_q ^p ]=ln(((1+p)/(1+q))) ∫_0 ^1 ((x^p −x^q )/(lnx))dx=ln(((1+p)/(1+q)))=ln(1+p)−ln(1+q) now put q=0 both side ∫_0 ^1 ((x^p −1)/(lnx))dx=ln(1+p) ans](Q47891.png)
$${we}\:{know} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx}=\mid\frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$ $${now}\:{intregate}\:{both}\:{side}\:{w}.{r}.{t}\:{k}\:{in}\:{the}\:{interval} \\ $$ $${say}\:{q}\:{to}\:{p} \\ $$ $$\int_{{q}} ^{{p}} {dk}\left[\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx}\right]=\int_{{q}} ^{{p}} \frac{{dk}}{\mathrm{1}+{k}} \\ $$ $${taking}\:{help}\:{from}\:{advanced}\:{level}\:{intregation} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} {dx}\int_{{q}} ^{{p}} {x}^{{k}} {dk}=\mid{ln}\left(\mathrm{1}+{k}\right)\mid_{{q}} ^{{p}} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} {dx}\left[\mid\frac{{x}^{{k}} }{{lnx}}\mid_{{q}} ^{{p}} \right]={ln}\left(\frac{\mathrm{1}+{p}}{\mathrm{1}+{q}}\right) \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} −{x}^{{q}} }{{lnx}}{dx}={ln}\left(\frac{\mathrm{1}+{p}}{\mathrm{1}+{q}}\right)={ln}\left(\mathrm{1}+{p}\right)−{ln}\left(\mathrm{1}+{q}\right) \\ $$ $${now}\:{put}\:{q}=\mathrm{0}\:{both}\:{side} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{p}} −\mathrm{1}}{{lnx}}{dx}={ln}\left(\mathrm{1}+{p}\right)\:{ans} \\ $$
