
Question Number 4785 by Dnilka228 last updated on 10/Mar/16
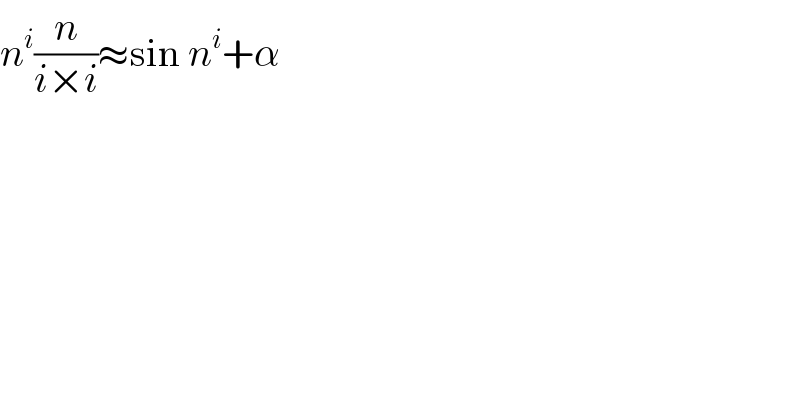
$${n}^{{i}} \frac{{n}}{{i}×{i}}\approx\mathrm{sin}\:{n}^{{i}} +\alpha \\ $$
Commented by Dnilka228 last updated on 10/Mar/16
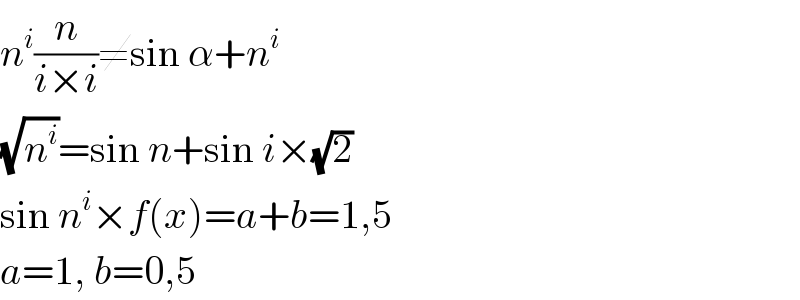
$${n}^{{i}} \frac{{n}}{{i}×{i}}\neq\mathrm{sin}\:\alpha+{n}^{{i}} \\ $$$$\sqrt{{n}^{{i}} }=\mathrm{sin}\:{n}+\mathrm{sin}\:{i}×\sqrt{\mathrm{2}} \\ $$$$\mathrm{sin}\:{n}^{{i}} ×{f}\left({x}\right)={a}+{b}=\mathrm{1},\mathrm{5} \\ $$$${a}=\mathrm{1},\:{b}=\mathrm{0},\mathrm{5} \\ $$
Commented by Dnilka228 last updated on 10/Mar/16
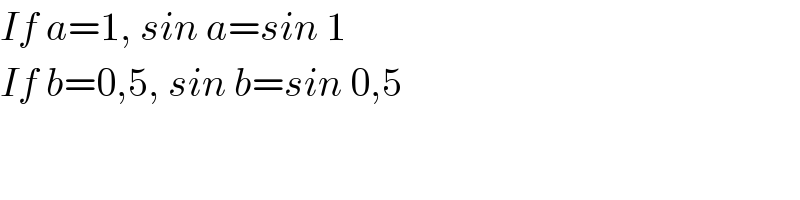
$${If}\:{a}=\mathrm{1},\:{sin}\:{a}={sin}\:\mathrm{1} \\ $$$${If}\:{b}=\mathrm{0},\mathrm{5},\:{sin}\:{b}={sin}\:\mathrm{0},\mathrm{5} \\ $$
