
Question Number 47775 by behi83417@gmail.com last updated on 14/Nov/18
Commented by behi83417@gmail.com last updated on 14/Nov/18
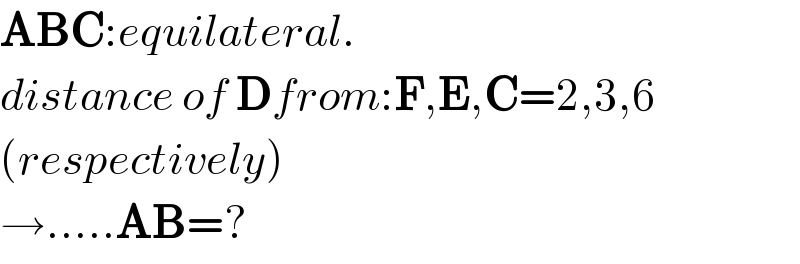
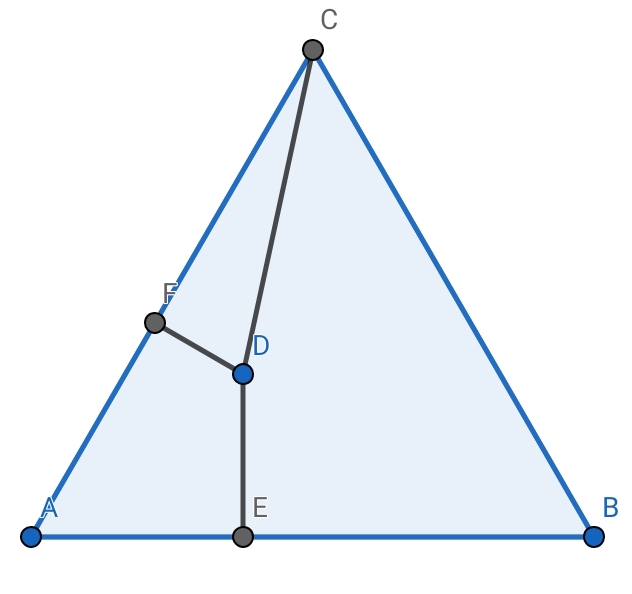
$$\boldsymbol{\mathrm{ABC}}:{equilateral}. \\ $$$${distance}\:{of}\:\boldsymbol{\mathrm{D}}{from}:\boldsymbol{\mathrm{F}},\boldsymbol{\mathrm{E}},\boldsymbol{\mathrm{C}}=\mathrm{2},\mathrm{3},\mathrm{6} \\ $$$$\left({respectively}\right) \\ $$$$\rightarrow.....\boldsymbol{\mathrm{AB}}=? \\ $$
Answered by behi83417@gmail.com last updated on 14/Nov/18
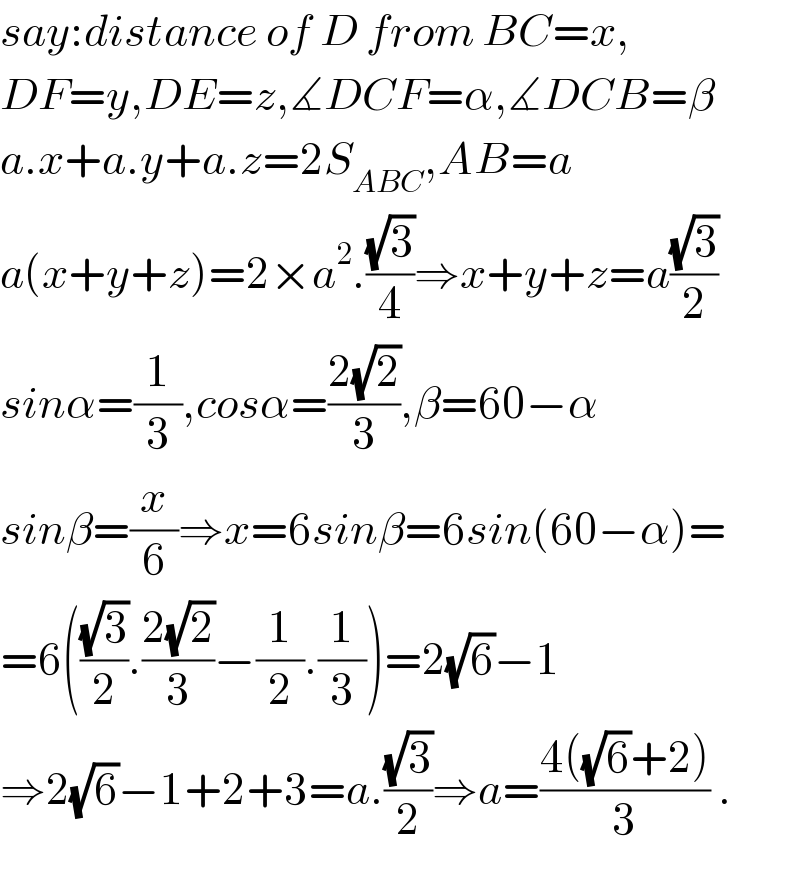
$${say}:{distance}\:{of}\:{D}\:{from}\:{BC}={x}, \\ $$$${DF}={y},{DE}={z},\measuredangle{DCF}=\alpha,\measuredangle{DCB}=\beta \\ $$$${a}.{x}+{a}.{y}+{a}.{z}=\mathrm{2}{S}_{{ABC}} ,{AB}={a} \\ $$$${a}\left({x}+{y}+{z}\right)=\mathrm{2}×{a}^{\mathrm{2}} .\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\Rightarrow{x}+{y}+{z}={a}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${sin}\alpha=\frac{\mathrm{1}}{\mathrm{3}},{cos}\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}},\beta=\mathrm{60}−\alpha \\ $$$${sin}\beta=\frac{{x}}{\mathrm{6}}\Rightarrow{x}=\mathrm{6}{sin}\beta=\mathrm{6}{sin}\left(\mathrm{60}−\alpha\right)= \\ $$$$=\mathrm{6}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{1}+\mathrm{2}+\mathrm{3}={a}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow{a}=\frac{\mathrm{4}\left(\sqrt{\mathrm{6}}+\mathrm{2}\right)}{\mathrm{3}}\:. \\ $$
Answered by mr W last updated on 14/Nov/18
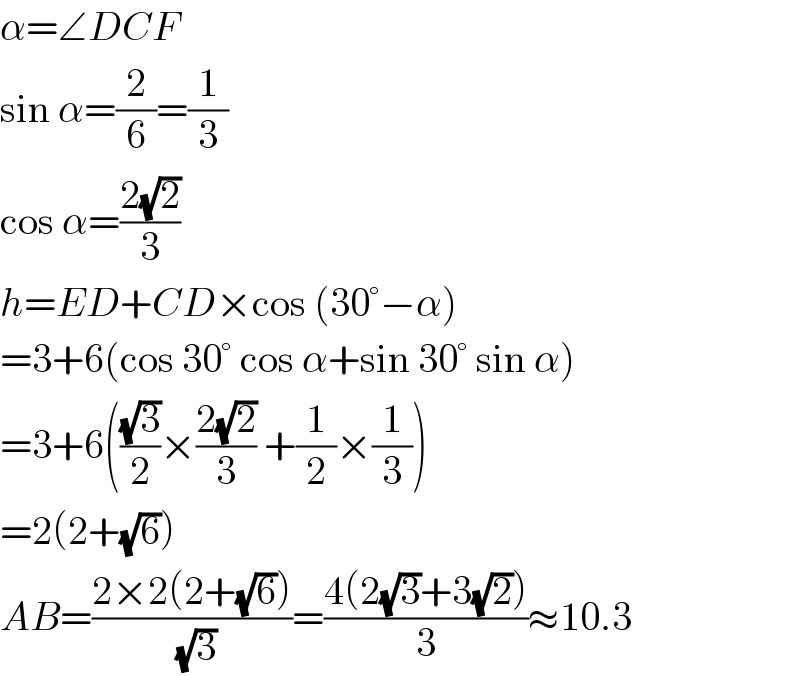
$$\alpha=\angle{DCF} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{2}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${h}={ED}+{CD}×\mathrm{cos}\:\left(\mathrm{30}°−\alpha\right) \\ $$$$=\mathrm{3}+\mathrm{6}\left(\mathrm{cos}\:\mathrm{30}°\:\mathrm{cos}\:\alpha+\mathrm{sin}\:\mathrm{30}°\:\mathrm{sin}\:\alpha\right) \\ $$$$=\mathrm{3}+\mathrm{6}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{6}}\right) \\ $$$${AB}=\frac{\mathrm{2}×\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{6}}\right)}{\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}\right)}{\mathrm{3}}\approx\mathrm{10}.\mathrm{3} \\ $$
Commented by behi83417@gmail.com last updated on 14/Nov/18
$${correct}\:{answer}.{thanks}\:{in}\:{advance}\:{sir}. \\ $$
