
Question Number 47725 by Meritguide1234 last updated on 14/Nov/18
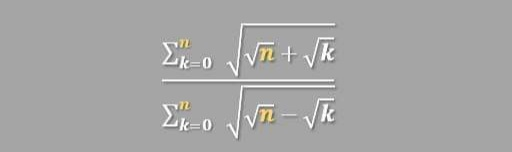
Commented by Meritguide1234 last updated on 15/Nov/18
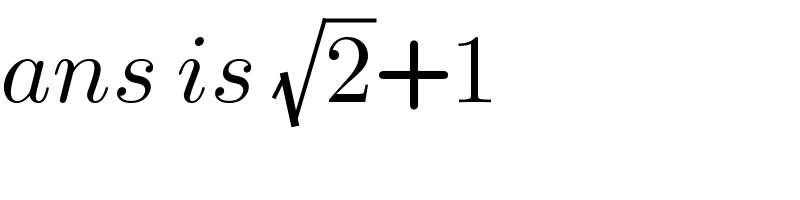
$${ans}\:{is}\:\sqrt{\mathrm{2}}+\mathrm{1} \\ $$
Commented by maxmathsup by imad last updated on 15/Nov/18
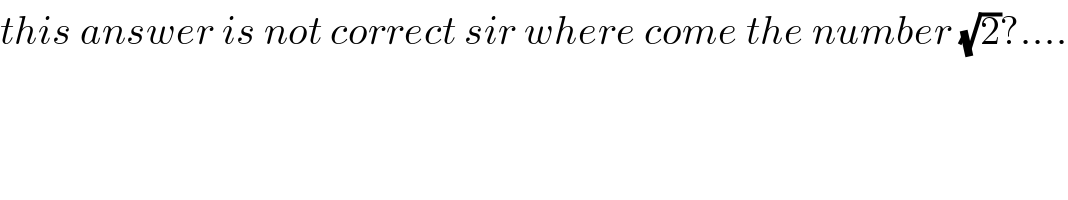
$${this}\:{answer}\:{is}\:{not}\:{correct}\:{sir}\:{where}\:{come}\:{the}\:{number}\:\sqrt{\mathrm{2}}?.... \\ $$
Answered by maxmathsup by imad last updated on 15/Nov/18
![if the Q. is find lim_(n→+∞) ((Σ_(k=0) ^n (√((√n)+(√k))))/(Σ_(k=0) ^n (√((√n)−(√k))))) let S_n =((Σ_(k=0) ^n (√((√n)+(√k))))/(Σ_(k=0) ^n (√((√n)−(√k))))) we have S_n =((n^(1/4) Σ_(k=0) ^n (√(1+(√(k/n)))))/(n^(1/4) (√(1−(√(k/n)))))) =(((1/n)Σ_(k=0) ^n (√(1+(√(k/n)))))/((1/(n ))Σ_(k=0) ^n (√(1−(√(k/n)))))) so S_n is a Rieman sum and lim_(n→+∞) S_n =((∫_0 ^1 (√(1+(√x)))dx)/(∫_0 ^1 (√(1−(√x)))dx)) let calculate ∫_0 ^1 (√(1+(√x)))dx changement (√(1+(√x)))=t give 1+(√x)=t^2 ⇒(√x)=t^2 −1 ⇒x=(t^2 −1)^2 =t^4 −2t^2 +1 ⇒ dx=4t^3 −4t)dt ⇒∫_0 ^1 (√(1+(√x)))dx =∫_1 ^2 t(4t^3 −4t)dt =4 ∫_1 ^2 (t^4 −t^2 )dt =4[(t^5 /5) −(t^3 /3)]_1 ^2 =4 {(2^5 /5) −(2^3 /3) } =32{ (4/5) −(1/3)} =32.(7/(15)) =((224)/(15)) now let calculate ∫_0 ^1 (√(1−(√x)))dx changement (√(1−(√x)))=t give 1−(√x)=t^2 ⇒(√x)=1−t^2 ⇒ x=(1−t^2 )^2 =t^4 −2t^2 +1 ⇒dx =(4t^3 −4t)dt ⇒ ∫_0 ^1 (√(1−(√x)))dx = −∫_0 ^1 t(4t^3 −4t)dt =−4 ∫_0 ^1 (t^4 −t^2 )dt =4 ∫_0 ^1 (t^2 −t^4 )dt =4[(t^3 /3) −(t^5 /5)]_0 ^1 =4{(1/3) −(1/5)}=4.(2/(15)) =(8/(15)) ⇒ lim_(n→+∞) S_n =((224)/8) =((112)/4) =((56)/2) =28 .](Q47853.png)
$${if}\:{the}\:{Q}.\:{is}\:{find}\:{lim}_{{n}\rightarrow+\infty} \frac{\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\sqrt{{n}}+\sqrt{{k}}}}{\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\sqrt{{n}}−\sqrt{{k}}}}\:{let}\:{S}_{{n}} =\frac{\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\sqrt{{n}}+\sqrt{{k}}}}{\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\sqrt{{n}}−\sqrt{{k}}}} \\ $$$${we}\:{have}\:{S}_{{n}} =\frac{{n}^{\frac{\mathrm{1}}{\mathrm{4}}} \sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\mathrm{1}+\sqrt{\frac{{k}}{{n}}}}}{{n}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{\mathrm{1}−\sqrt{\frac{{k}}{{n}}}}}\:=\frac{\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\mathrm{1}+\sqrt{\frac{{k}}{{n}}}}}{\frac{\mathrm{1}}{{n}\:}\sum_{{k}=\mathrm{0}} ^{{n}} \sqrt{\mathrm{1}−\sqrt{\frac{{k}}{{n}}}}}\:{so}\:{S}_{{n}} {is}\:{a}\:{Rieman}\:{sum} \\ $$$${and}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\sqrt{{x}}}{dx}}{\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}}\:{let}\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}+\sqrt{{x}}}{dx}\:{changement} \\ $$$$\sqrt{\mathrm{1}+\sqrt{{x}}}={t}\:{give}\:\mathrm{1}+\sqrt{{x}}={t}^{\mathrm{2}} \:\Rightarrow\sqrt{{x}}={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow{x}=\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow \\ $$$$\left.{dx}=\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\sqrt{{x}}}{dx}\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:{t}\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt}\:=\mathrm{4}\:\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$=\mathrm{4}\left[\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\:−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4}\:\left\{\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{5}}\:−\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}\:\right\}\:=\mathrm{32}\left\{\:\frac{\mathrm{4}}{\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{3}}\right\}\:=\mathrm{32}.\frac{\mathrm{7}}{\mathrm{15}}\:=\frac{\mathrm{224}}{\mathrm{15}}\:\:{now}\:{let}\:{calculate} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\:{changement}\:\sqrt{\mathrm{1}−\sqrt{{x}}}={t}\:{give}\:\mathrm{1}−\sqrt{{x}}={t}^{\mathrm{2}} \:\Rightarrow\sqrt{{x}}=\mathrm{1}−{t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}=\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} ={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow{dx}\:=\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} {t}\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt}\: \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}^{\mathrm{2}} −{t}^{\mathrm{4}} \right){dt}\:=\mathrm{4}\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{4}\left\{\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{5}}\right\}=\mathrm{4}.\frac{\mathrm{2}}{\mathrm{15}}\:=\frac{\mathrm{8}}{\mathrm{15}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{224}}{\mathrm{8}}\:=\frac{\mathrm{112}}{\mathrm{4}}\:=\frac{\mathrm{56}}{\mathrm{2}}\:=\mathrm{28}\:. \\ $$$$ \\ $$
Commented by Meritguide1234 last updated on 16/Nov/18

Commented by Meritguide1234 last updated on 16/Nov/18
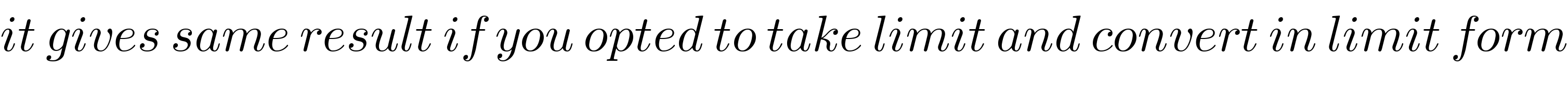
$${it}\:{gives}\:{same}\:{result}\:{if}\:{you}\:{opted}\:{to}\:{take}\:{limit}\:{and}\:{convert}\:{in}\:{limit}\:{form} \\ $$
