Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 47621 by rahul 19 last updated on 12/Nov/18

Find locus of point P from which tangents PA & PB to circles x^2 +y^2 =a^2 and x^2 +y^2 =b^2 respectively are perpendicular.

$${Find}\:{locus}\:{of}\:{point}\:{P}\:{from}\:{which} \\ $$ $${tangents}\:{PA}\:\&\:{PB}\:{to}\:{circles}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$ $${and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \:{respectively}\:{are}\:{perpendicular}. \\ $$

Commented byrahul 19 last updated on 12/Nov/18

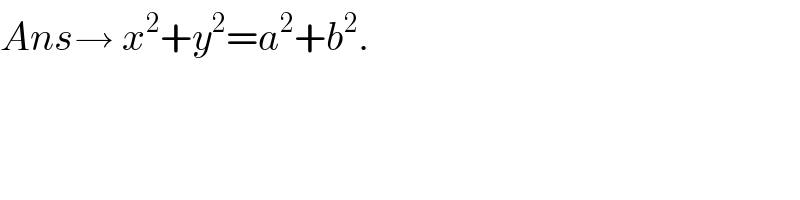
Ans→ x^2 +y^2 =a^2 +b^2 .

$${Ans}\rightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} . \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18

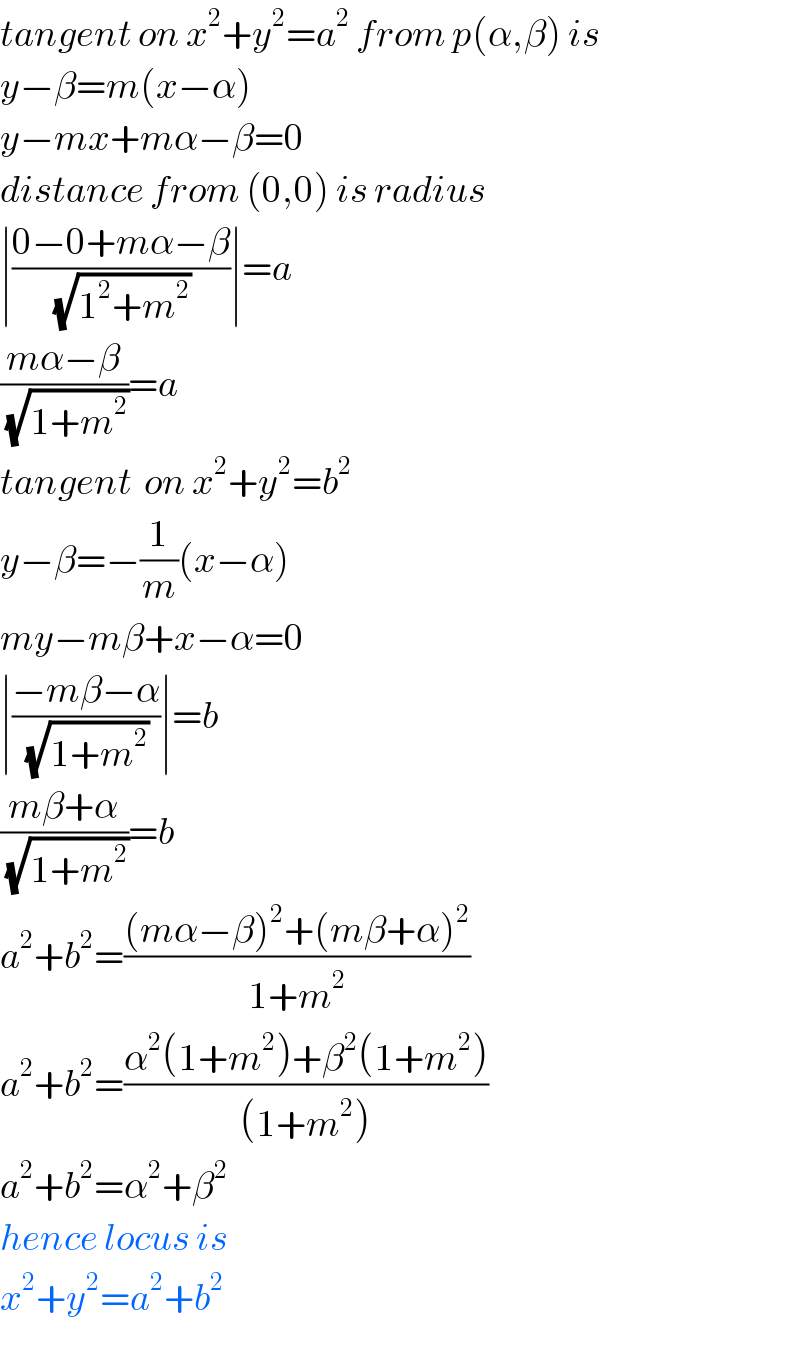
tangent on x^2 +y^2 =a^2 from p(α,β) is y−β=m(x−α) y−mx+mα−β=0 distance from (0,0) is radius ∣((0−0+mα−β)/(√(1^2 +m^2 )))∣=a ((mα−β)/(√(1+m^2 )))=a tangent on x^2 +y^2 =b^2 y−β=−(1/m)(x−α) my−mβ+x−α=0 ∣((−mβ−α)/(√(1+m^2 )))∣=b ((mβ+α)/(√(1+m^2 )))=b a^2 +b^2 =(((mα−β)^2 +(mβ+α)^2 )/(1+m^2 )) a^2 +b^2 =((α^2 (1+m^2 )+β^2 (1+m^2 ))/((1+m^2 ))) a^2 +b^2 =α^2 +β^2 hence locus is x^2 +y^2 =a^2 +b^2

$${tangent}\:{on}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \:{from}\:{p}\left(\alpha,\beta\right)\:{is} \\ $$ $${y}−\beta={m}\left({x}−\alpha\right) \\ $$ $${y}−{mx}+{m}\alpha−\beta=\mathrm{0} \\ $$ $${distance}\:{from}\:\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{radius} \\ $$ $$\mid\frac{\mathrm{0}−\mathrm{0}+{m}\alpha−\beta}{\sqrt{\mathrm{1}^{\mathrm{2}} +{m}^{\mathrm{2}} }}\mid={a} \\ $$ $$\frac{{m}\alpha−\beta}{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}={a} \\ $$ $${tangent}\:\:{on}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$ $${y}−\beta=−\frac{\mathrm{1}}{{m}}\left({x}−\alpha\right) \\ $$ $${my}−{m}\beta+{x}−\alpha=\mathrm{0} \\ $$ $$\mid\frac{−{m}\beta−\alpha}{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}\mid={b} \\ $$ $$\frac{{m}\beta+\alpha}{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}={b} \\ $$ $${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\left({m}\alpha−\beta\right)^{\mathrm{2}} +\left({m}\beta+\alpha\right)^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$ $${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\alpha^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)+\beta^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)} \\ $$ $${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$ $${hence}\:{locus}\:{is} \\ $$ $${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$

Commented byrahul 19 last updated on 13/Nov/18

thanks sir ����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com