
Question Number 47552 by ggny last updated on 11/Nov/18
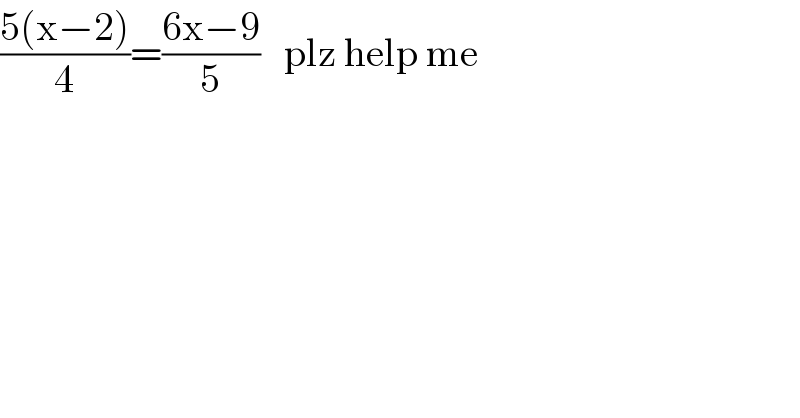
$$\frac{\mathrm{5}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{4}}=\frac{\mathrm{6x}−\mathrm{9}}{\mathrm{5}}\:\:\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by maxmathsup by imad last updated on 11/Nov/18
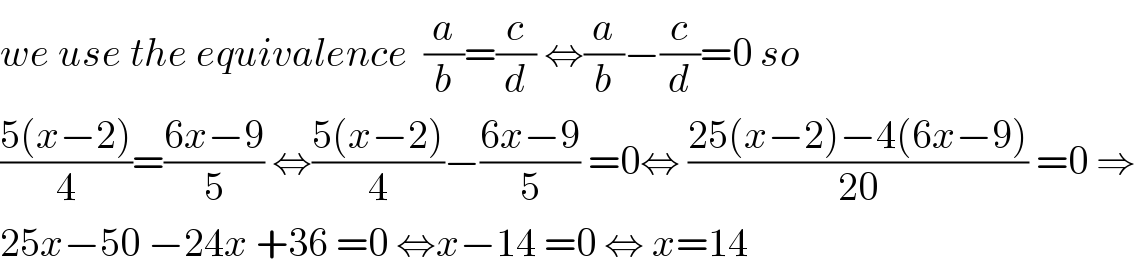
$${we}\:{use}\:{the}\:{equivalence}\:\:\frac{{a}}{{b}}=\frac{{c}}{{d}}\:\Leftrightarrow\frac{{a}}{{b}}−\frac{{c}}{{d}}=\mathrm{0}\:{so} \\ $$$$\frac{\mathrm{5}\left({x}−\mathrm{2}\right)}{\mathrm{4}}=\frac{\mathrm{6}{x}−\mathrm{9}}{\mathrm{5}}\:\Leftrightarrow\frac{\mathrm{5}\left({x}−\mathrm{2}\right)}{\mathrm{4}}−\frac{\mathrm{6}{x}−\mathrm{9}}{\mathrm{5}}\:=\mathrm{0}\Leftrightarrow\:\frac{\mathrm{25}\left({x}−\mathrm{2}\right)−\mathrm{4}\left(\mathrm{6}{x}−\mathrm{9}\right)}{\mathrm{20}}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{25}{x}−\mathrm{50}\:−\mathrm{24}{x}\:+\mathrm{36}\:=\mathrm{0}\:\Leftrightarrow{x}−\mathrm{14}\:=\mathrm{0}\:\Leftrightarrow\:{x}=\mathrm{14} \\ $$
Answered by $@ty@m last updated on 11/Nov/18

Commented by $@ty@m last updated on 11/Nov/18
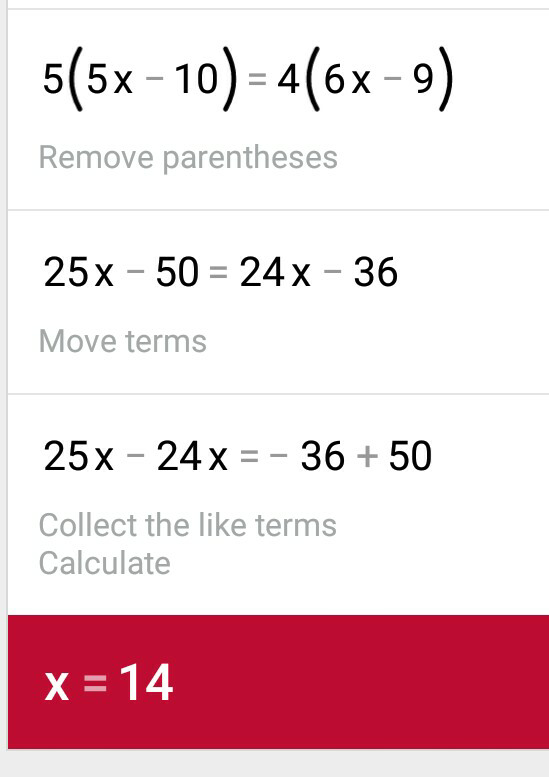
Answered by peter frank last updated on 11/Nov/18
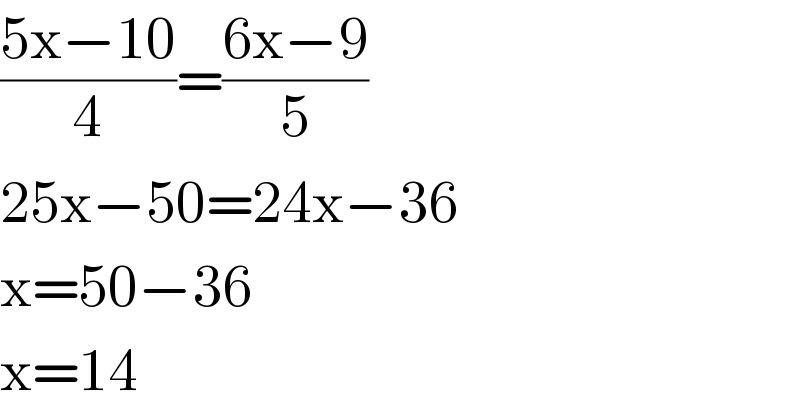
$$\frac{\mathrm{5x}−\mathrm{10}}{\mathrm{4}}=\frac{\mathrm{6x}−\mathrm{9}}{\mathrm{5}} \\ $$$$\mathrm{25x}−\mathrm{50}=\mathrm{24x}−\mathrm{36} \\ $$$$\mathrm{x}=\mathrm{50}−\mathrm{36} \\ $$$$\mathrm{x}=\mathrm{14} \\ $$
Answered by Rio Michael last updated on 11/Nov/18
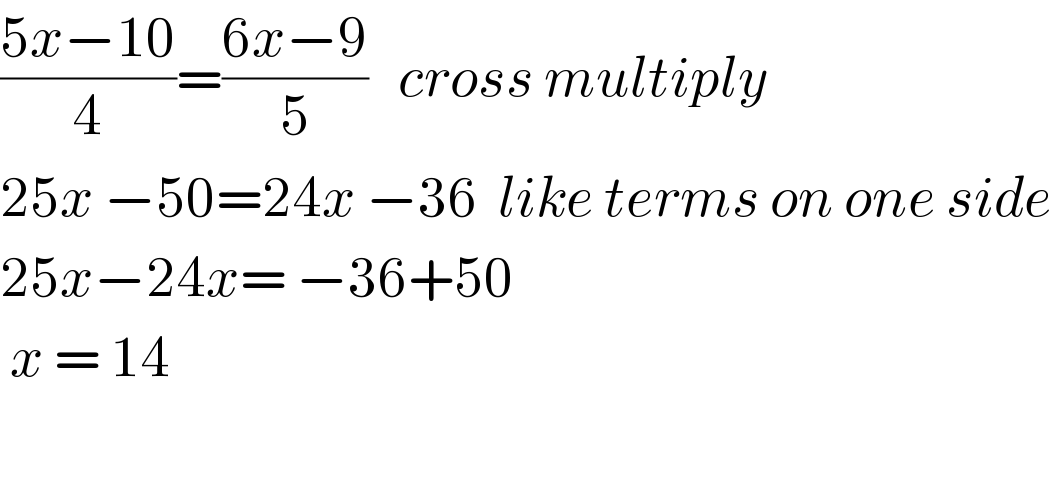
$$\frac{\mathrm{5}{x}−\mathrm{10}}{\mathrm{4}}=\frac{\mathrm{6}{x}−\mathrm{9}}{\mathrm{5}}\:\:\:{cross}\:{multiply} \\ $$$$\mathrm{25}{x}\:−\mathrm{50}=\mathrm{24}{x}\:−\mathrm{36}\:\:{like}\:{terms}\:{on}\:{one}\:{side} \\ $$$$\mathrm{25}{x}−\mathrm{24}{x}=\:−\mathrm{36}+\mathrm{50} \\ $$$$\:{x}\:=\:\mathrm{14} \\ $$$$ \\ $$
