
Question Number 47476 by hassentimol last updated on 10/Nov/18
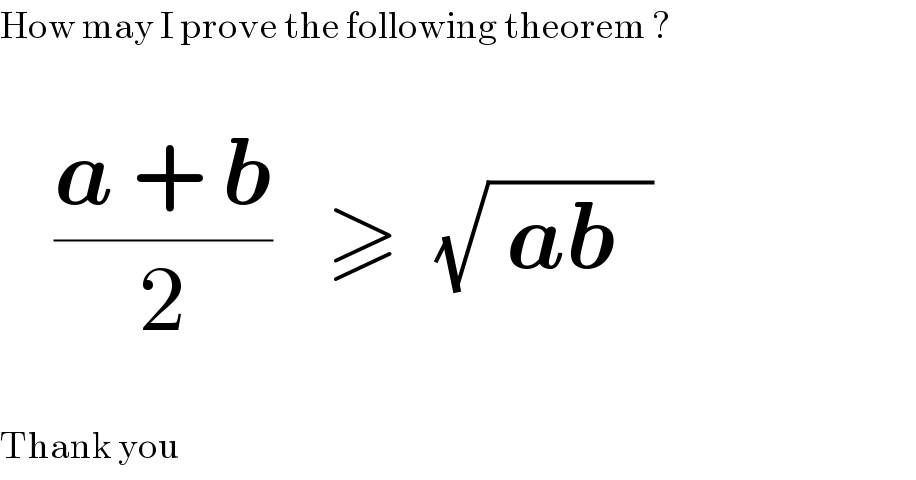
$$\mathrm{How}\:\mathrm{may}\:\mathrm{I}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{following}\:\mathrm{theorem}\:? \\ $$$$ \\ $$$$\:\:\:\frac{\boldsymbol{{a}}\:+\:\boldsymbol{{b}}}{\mathrm{2}}\:\:\:\geqslant\:\:\sqrt{\:\boldsymbol{{ab}}\:\:} \\ $$$$ \\ $$$$\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by prakash jain last updated on 11/Nov/18
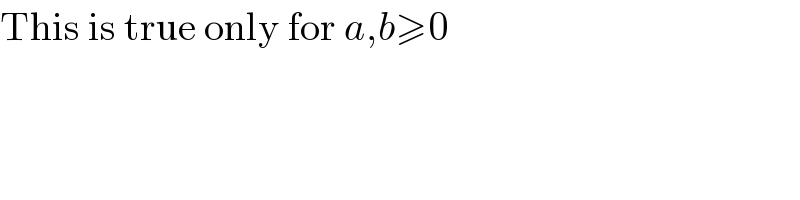
$$\mathrm{This}\:\mathrm{is}\:\mathrm{true}\:\mathrm{only}\:\mathrm{for}\:{a},{b}\geqslant\mathrm{0} \\ $$
Answered by Joel578 last updated on 11/Nov/18
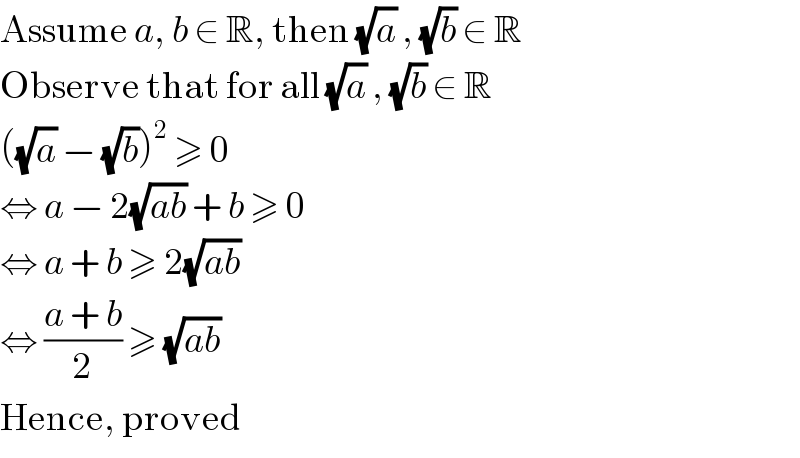
$$\mathrm{Assume}\:{a},\:{b}\:\in\:\mathbb{R},\:\mathrm{then}\:\sqrt{{a}}\:,\:\sqrt{{b}}\:\in\:\mathbb{R} \\ $$$$\mathrm{Observe}\:\mathrm{that}\:\mathrm{for}\:\mathrm{all}\:\sqrt{{a}}\:,\:\sqrt{{b}}\:\in\:\mathbb{R} \\ $$$$\left(\sqrt{{a}}\:−\:\sqrt{{b}}\right)^{\mathrm{2}} \:\geqslant\:\mathrm{0} \\ $$$$\Leftrightarrow\:{a}\:−\:\mathrm{2}\sqrt{{ab}}\:+\:{b}\:\geqslant\:\mathrm{0} \\ $$$$\Leftrightarrow\:{a}\:+\:{b}\:\geqslant\:\mathrm{2}\sqrt{{ab}} \\ $$$$\Leftrightarrow\:\frac{{a}\:+\:{b}}{\mathrm{2}}\:\geqslant\:\sqrt{{ab}} \\ $$$$\mathrm{Hence},\:\mathrm{proved} \\ $$
Commented by hassentimol last updated on 11/Nov/18
$$ \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}\:! \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{also}\:\mathrm{very}\:\mathrm{helpful}\:! \\ $$
Answered by .... last updated on 10/Nov/18
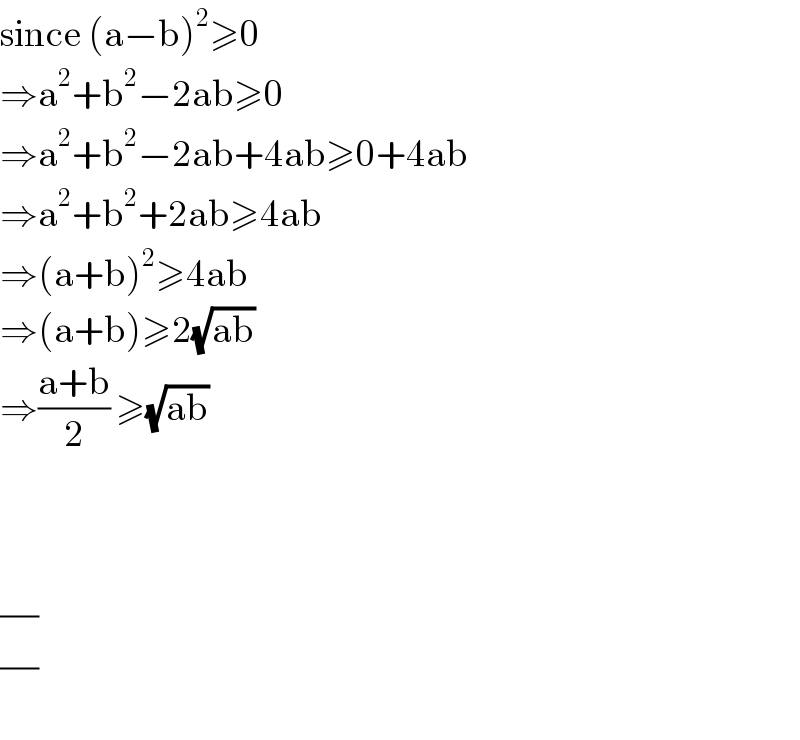
$$\mathrm{since}\:\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}+\mathrm{4ab}\geqslant\mathrm{0}+\mathrm{4ab} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2ab}\geqslant\mathrm{4ab} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \geqslant\mathrm{4ab} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\geqslant\mathrm{2}\sqrt{\mathrm{ab}} \\ $$$$\Rightarrow\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\:\geqslant\sqrt{\mathrm{ab}} \\ $$$$ \\ $$$$ \\ $$$$\frac{\frac{}{}}{} \\ $$
Commented by hassentimol last updated on 11/Nov/18

$$ \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{very}\:\mathrm{helpful}\:! \\ $$
