
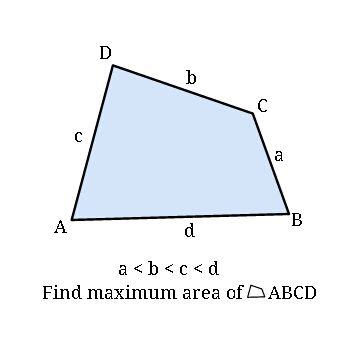
Question Number 47407 by ajfour last updated on 09/Nov/18
Answered by ajfour last updated on 10/Nov/18
![let BD = x , ∠A = φ, ∠C = θ S_(ABCD) = ((absin θ)/2)+((cdsin φ)/2) x^2 = a^2 +b^2 −2abcos θ = c^2 +d^2 −2cdcos φ ⇒ (absin θ)(dθ/dx) = (cdsin φ)(dφ/dx) = 2x (dS/dx) = 0 ⇒ (abcos θ)(dθ/dx)+(cdcos φ)(dφ/dx)=0 ⇒ cos θ+(cos φ)(((sin θ)/(sin φ)))= 0 ⇒ θ+φ = π ⇒ a^2 +b^2 −2abcos θ = c^2 +d^2 +2cdcos θ or cos θ = ((a^2 +b^2 −c^2 −d^2 )/(2(ab+cd))) (S_(ABCD) )_(max) = ((sin θ)/2)(ab+cd) = (((ab+cd))/2)(√(1−[((a^2 +b^2 −c^2 −d^2 )/(2(ab+cd)))]^2 )) S_(max) = (1/4)(√(4(ab+cd)^2 −[(a^2 +b^2 )−(c^2 +d^2 )]^2 )) .](Q47408.png)
$${let}\:{BD}\:=\:{x}\:,\:\angle{A}\:=\:\phi,\:\angle{C}\:=\:\theta \\ $$$${S}_{{ABCD}} \:=\:\frac{{ab}\mathrm{sin}\:\theta}{\mathrm{2}}+\frac{{cd}\mathrm{sin}\:\phi}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:=\:{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\mathrm{cos}\:\phi \\ $$$$\Rightarrow\:\left({ab}\mathrm{sin}\:\theta\right)\frac{{d}\theta}{{dx}}\:=\:\left({cd}\mathrm{sin}\:\phi\right)\frac{{d}\phi}{{dx}}\:=\:\mathrm{2}{x} \\ $$$$\frac{{dS}}{{dx}}\:=\:\mathrm{0}\:\Rightarrow \\ $$$$\:\:\:\left({ab}\mathrm{cos}\:\theta\right)\frac{{d}\theta}{{dx}}+\left({cd}\mathrm{cos}\:\phi\right)\frac{{d}\phi}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta+\left(\mathrm{cos}\:\phi\right)\left(\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:\phi}\right)=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\theta+\phi\:=\:\pi \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\theta\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +\mathrm{2}{cd}\mathrm{cos}\:\theta \\ $$$${or}\:\:\:\:\mathrm{cos}\:\theta\:=\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}\left({ab}+{cd}\right)} \\ $$$$\left({S}_{{ABCD}} \right)_{{max}} \:=\:\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\left({ab}+{cd}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\left({ab}+{cd}\right)}{\mathrm{2}}\sqrt{\mathrm{1}−\left[\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}\left({ab}+{cd}\right)}\right]^{\mathrm{2}} }\: \\ $$$$\:\:{S}_{{max}} =\:\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}\left({ab}+{cd}\right)^{\mathrm{2}} −\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)\right]^{\mathrm{2}} }\:. \\ $$
Commented by mr W last updated on 10/Nov/18

$${thank}\:{you}\:{sir}! \\ $$$${it}\:{shows}\:{the}\:{area}\:{reaches}\:{maximum} \\ $$$${when}\:{the}\:{quadrilateral}\:{is}\:{inscribed}\:{in} \\ $$$${a}\:{circle}. \\ $$
