
Question Number 47394 by gunawan last updated on 09/Nov/18
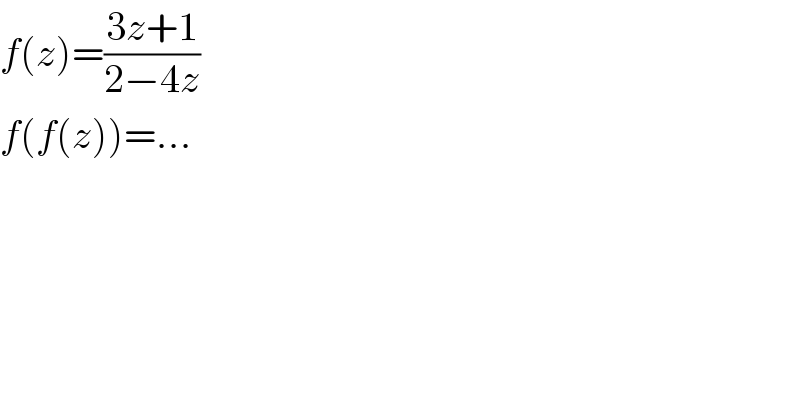
$${f}\left({z}\right)=\frac{\mathrm{3}{z}+\mathrm{1}}{\mathrm{2}−\mathrm{4}{z}} \\ $$$${f}\left({f}\left({z}\right)\right)=... \\ $$
Commented by maxmathsup by imad last updated on 10/Nov/18
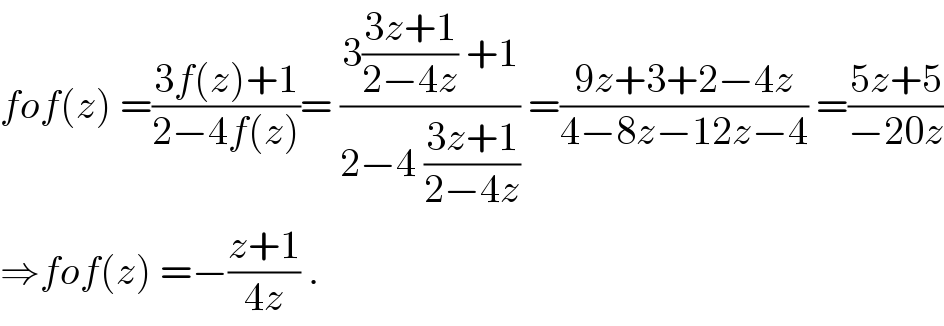
$${fof}\left({z}\right)\:=\frac{\mathrm{3}{f}\left({z}\right)+\mathrm{1}}{\mathrm{2}−\mathrm{4}{f}\left({z}\right)}=\:\frac{\mathrm{3}\frac{\mathrm{3}{z}+\mathrm{1}}{\mathrm{2}−\mathrm{4}{z}}\:+\mathrm{1}}{\mathrm{2}−\mathrm{4}\:\frac{\mathrm{3}{z}+\mathrm{1}}{\mathrm{2}−\mathrm{4}{z}}}\:=\frac{\mathrm{9}{z}+\mathrm{3}+\mathrm{2}−\mathrm{4}{z}}{\mathrm{4}−\mathrm{8}{z}−\mathrm{12}{z}−\mathrm{4}}\:=\frac{\mathrm{5}{z}+\mathrm{5}}{−\mathrm{20}{z}} \\ $$$$\Rightarrow{fof}\left({z}\right)\:=−\frac{{z}+\mathrm{1}}{\mathrm{4}{z}}\:. \\ $$
Answered by ajfour last updated on 09/Nov/18
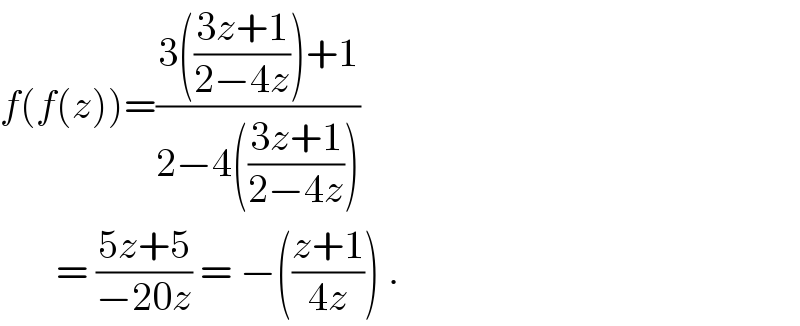
$${f}\left({f}\left({z}\right)\right)=\frac{\mathrm{3}\left(\frac{\mathrm{3}{z}+\mathrm{1}}{\mathrm{2}−\mathrm{4}{z}}\right)+\mathrm{1}}{\mathrm{2}−\mathrm{4}\left(\frac{\mathrm{3}{z}+\mathrm{1}}{\mathrm{2}−\mathrm{4}{z}}\right)} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{5}{z}+\mathrm{5}}{−\mathrm{20}{z}}\:=\:−\left(\frac{{z}+\mathrm{1}}{\mathrm{4}{z}}\right)\:. \\ $$
