
Question Number 47248 by maxmathsup by imad last updated on 06/Nov/18
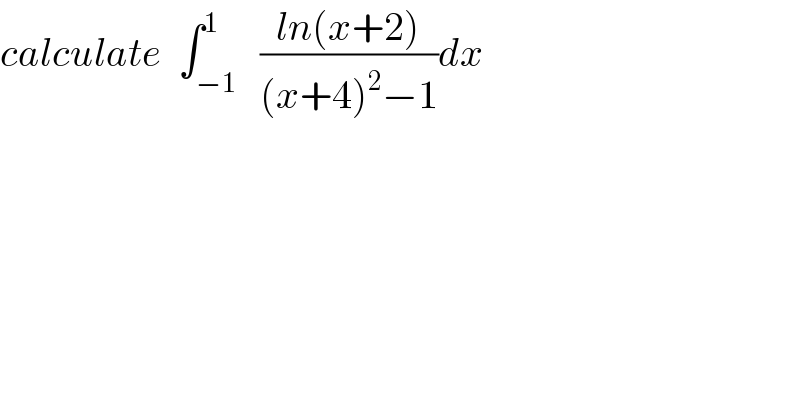
$${calculate}\:\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}+\mathrm{2}\right)}{\left({x}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 16/Nov/18
![let A = ∫_(−1) ^1 ((ln(x+2))/((x+4)^2 −1))dx ⇒ A =_(x+2=t) ∫_1 ^3 ((ln(t))/((t+2)^2 −1))dt =∫_1 ^3 ((ln(t))/((t+1)(t+3)))dt =(1/2)∫_1 ^3 {(1/(t+1)) −(1/(t+3))}ln(t)dt =(1/2) ∫_1 ^3 ((ln(t))/(t+1))dt −(1/2) ∫_1 ^3 ((ln(t))/(t+3))dt let determine ∫ ((ln(x))/(x+1))dx the calculator give ∫ ((ln(x))/(x+1)) dx=ln(x)ln(x+1) +L_(i 2) (−x) ⇒ ∫_1 ^3 ((ln(t))/(t+1))dt =[ln(t)ln(t+1)+L_(i2) (−t)]_1 ^3 =2ln(3)ln(2) +L_(i2) (−3) −L_(i2) (−1) also ∫ ((ln(x))/(x+3))dx =ln(x)ln((x/3)+1)+L_(i2) (−(x/3)) ⇒ ∫_1 ^3 ((ln(x))/(x+3)) =[ln(x)ln((x/3)+1)+L_(i2) (−(x/3))]_1 ^3 =ln(3)ln(2)+L_(i2) (−1)−L_(i2) (−(1/3))....](Q47873.png)
$${let}\:{A}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{{ln}\left({x}+\mathrm{2}\right)}{\left({x}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{1}}{dx}\:\Rightarrow\:{A}\:=_{{x}+\mathrm{2}={t}} \:\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right)}{\left({t}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{ln}\left({t}\right)}{\left({t}+\mathrm{1}\right)\left({t}+\mathrm{3}\right)}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{3}} \left\{\frac{\mathrm{1}}{{t}+\mathrm{1}}\:−\frac{\mathrm{1}}{{t}+\mathrm{3}}\right\}{ln}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{ln}\left({t}\right)}{{t}+\mathrm{1}}{dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{ln}\left({t}\right)}{{t}+\mathrm{3}}{dt}\:\:\:{let}\:{determine}\:\int\:\:\frac{{ln}\left({x}\right)}{{x}+\mathrm{1}}{dx}\:{the}\:{calculator} \\ $$$${give}\:\int\:\frac{{ln}\left({x}\right)}{{x}+\mathrm{1}}\:{dx}={ln}\left({x}\right){ln}\left({x}+\mathrm{1}\right)\:+{L}_{{i}\:\mathrm{2}} \left(−{x}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{ln}\left({t}\right)}{{t}+\mathrm{1}}{dt}\:=\left[{ln}\left({t}\right){ln}\left({t}+\mathrm{1}\right)+{L}_{{i}\mathrm{2}} \left(−{t}\right)\right]_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{2}{ln}\left(\mathrm{3}\right){ln}\left(\mathrm{2}\right)\:+{L}_{{i}\mathrm{2}} \left(−\mathrm{3}\right) \\ $$$$−{L}_{{i}\mathrm{2}} \left(−\mathrm{1}\right)\:\:{also}\:\:\int\:\:\frac{{ln}\left({x}\right)}{{x}+\mathrm{3}}{dx}\:={ln}\left({x}\right){ln}\left(\frac{{x}}{\mathrm{3}}+\mathrm{1}\right)+{L}_{{i}\mathrm{2}} \left(−\frac{{x}}{\mathrm{3}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{ln}\left({x}\right)}{{x}+\mathrm{3}}\:=\left[{ln}\left({x}\right){ln}\left(\frac{{x}}{\mathrm{3}}+\mathrm{1}\right)+{L}_{{i}\mathrm{2}} \left(−\frac{{x}}{\mathrm{3}}\right)\right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$={ln}\left(\mathrm{3}\right){ln}\left(\mathrm{2}\right)+{L}_{{i}\mathrm{2}} \left(−\mathrm{1}\right)−{L}_{{i}\mathrm{2}} \left(−\frac{\mathrm{1}}{\mathrm{3}}\right).... \\ $$
