
Question Number 472 by 123456 last updated on 25/Jan/15
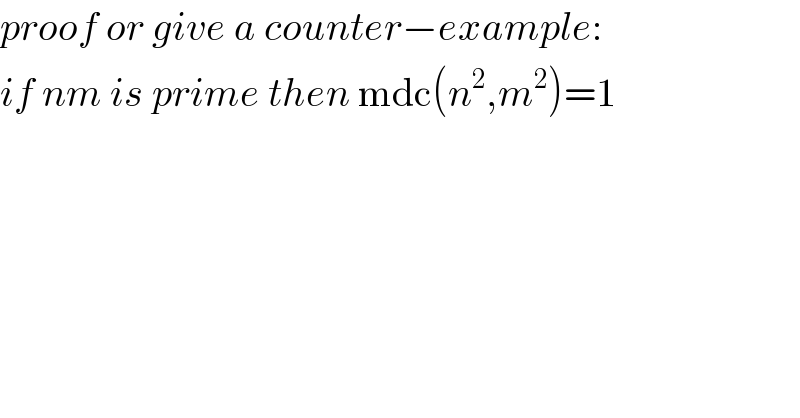
$${proof}\:{or}\:{give}\:{a}\:{counter}−{example}: \\ $$$${if}\:{nm}\:{is}\:{prime}\:{then}\:\mathrm{mdc}\left({n}^{\mathrm{2}} ,{m}^{\mathrm{2}} \right)=\mathrm{1} \\ $$
Answered by prakash jain last updated on 10/Jan/15
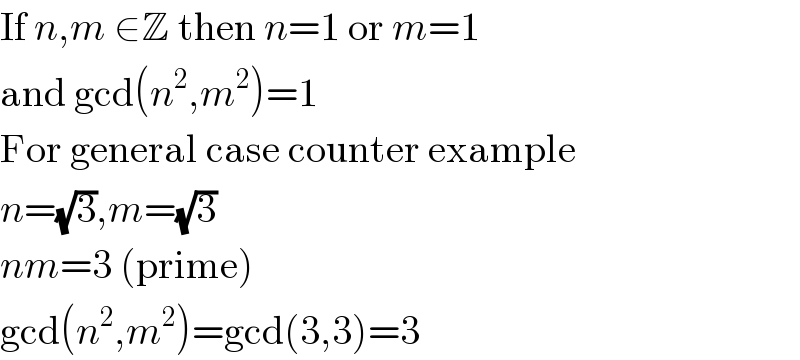
$$\mathrm{If}\:{n},{m}\:\in\mathbb{Z}\:\mathrm{then}\:{n}=\mathrm{1}\:\mathrm{or}\:{m}=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{gcd}\left({n}^{\mathrm{2}} ,{m}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$$\mathrm{For}\:\mathrm{general}\:\mathrm{case}\:\mathrm{counter}\:\mathrm{example} \\ $$$${n}=\sqrt{\mathrm{3}},{m}=\sqrt{\mathrm{3}} \\ $$$${nm}=\mathrm{3}\:\left(\mathrm{prime}\right) \\ $$$$\mathrm{gcd}\left({n}^{\mathrm{2}} ,{m}^{\mathrm{2}} \right)=\mathrm{gcd}\left(\mathrm{3},\mathrm{3}\right)=\mathrm{3} \\ $$
