
Question Number 47145 by ajfour last updated on 05/Nov/18
Commented by ajfour last updated on 05/Nov/18
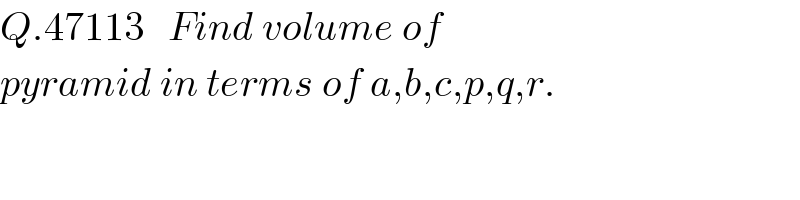
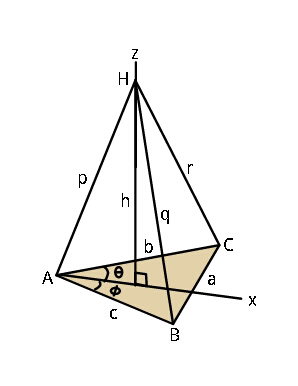
$${Q}.\mathrm{47113}\:\:\:{Find}\:{volume}\:{of} \\ $$$${pyramid}\:{in}\:{terms}\:{of}\:{a},{b},{c},{p},{q},{r}. \\ $$
Answered by ajfour last updated on 05/Nov/18
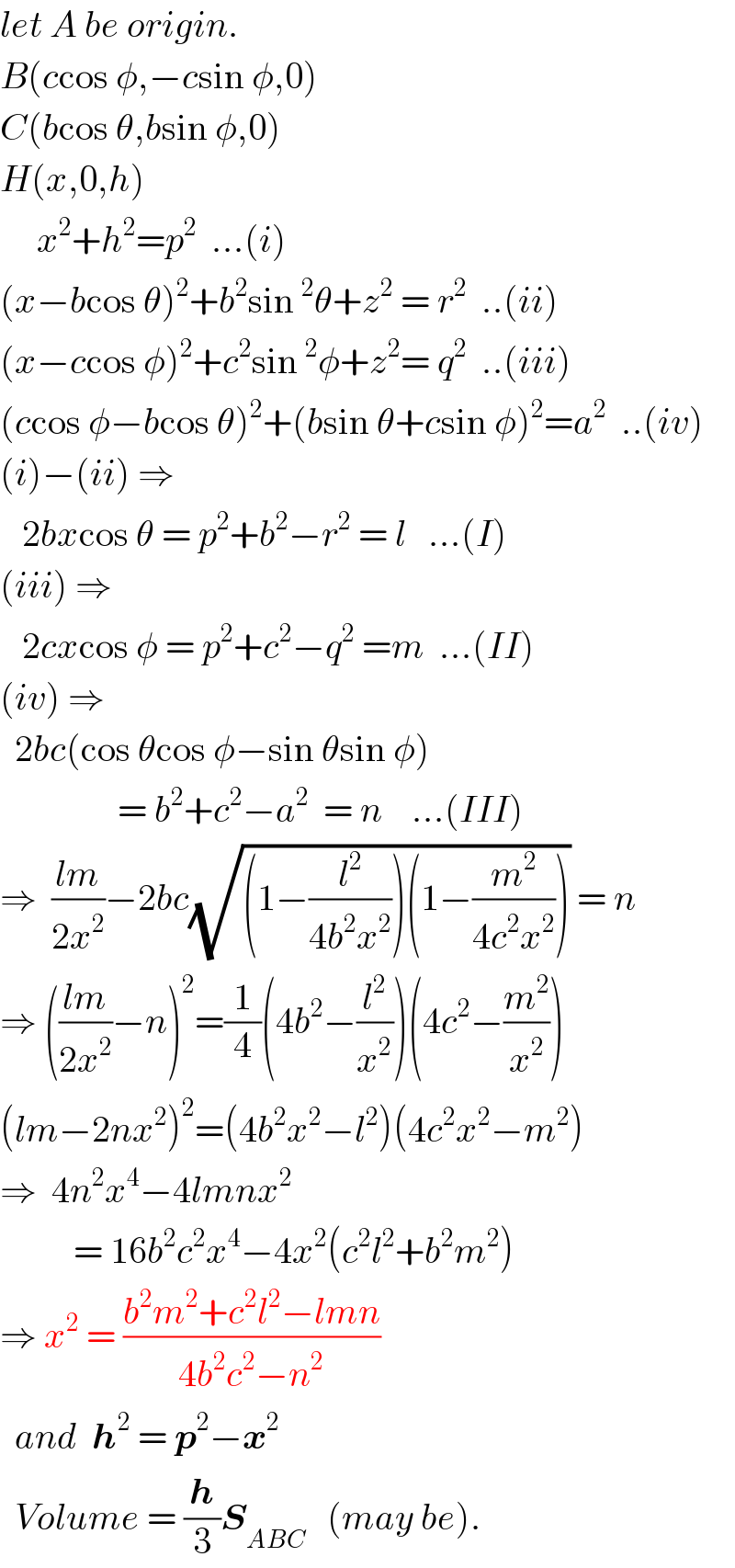
$${let}\:{A}\:{be}\:{origin}. \\ $$$${B}\left({c}\mathrm{cos}\:\phi,−{c}\mathrm{sin}\:\phi,\mathrm{0}\right) \\ $$$${C}\left({b}\mathrm{cos}\:\theta,{b}\mathrm{sin}\:\phi,\mathrm{0}\right) \\ $$$${H}\left({x},\mathrm{0},{h}\right) \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +{h}^{\mathrm{2}} ={p}^{\mathrm{2}} \:\:...\left({i}\right) \\ $$$$\left({x}−{b}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{z}^{\mathrm{2}} \:=\:{r}^{\mathrm{2}} \:\:..\left({ii}\right) \\ $$$$\left({x}−{c}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi+{z}^{\mathrm{2}} =\:{q}^{\mathrm{2}} \:\:..\left({iii}\right) \\ $$$$\left({c}\mathrm{cos}\:\phi−{b}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({b}\mathrm{sin}\:\theta+{c}\mathrm{sin}\:\phi\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \:\:..\left({iv}\right) \\ $$$$\left({i}\right)−\left({ii}\right)\:\Rightarrow \\ $$$$\:\:\:\mathrm{2}{bx}\mathrm{cos}\:\theta\:=\:{p}^{\mathrm{2}} +{b}^{\mathrm{2}} −{r}^{\mathrm{2}} \:=\:{l}\:\:\:...\left({I}\right) \\ $$$$\left({iii}\right)\:\Rightarrow \\ $$$$\:\:\:\mathrm{2}{cx}\mathrm{cos}\:\phi\:=\:{p}^{\mathrm{2}} +{c}^{\mathrm{2}} −{q}^{\mathrm{2}} \:={m}\:\:...\left({II}\right) \\ $$$$\left({iv}\right)\:\Rightarrow \\ $$$$\:\:\mathrm{2}{bc}\left(\mathrm{cos}\:\theta\mathrm{cos}\:\phi−\mathrm{sin}\:\theta\mathrm{sin}\:\phi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\:=\:{n}\:\:\:\:...\left({III}\right) \\ $$$$\Rightarrow\:\:\frac{{lm}}{\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{2}{bc}\sqrt{\left(\mathrm{1}−\frac{{l}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} {x}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{m}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} {x}^{\mathrm{2}} }\right)}\:=\:{n} \\ $$$$\Rightarrow\:\left(\frac{{lm}}{\mathrm{2}{x}^{\mathrm{2}} }−{n}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}{b}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)\left(\mathrm{4}{c}^{\mathrm{2}} −\frac{{m}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right) \\ $$$$\left({lm}−\mathrm{2}{nx}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{4}{b}^{\mathrm{2}} {x}^{\mathrm{2}} −{l}^{\mathrm{2}} \right)\left(\mathrm{4}{c}^{\mathrm{2}} {x}^{\mathrm{2}} −{m}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{4}{n}^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{4}{lmnx}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{16}{b}^{\mathrm{2}} {c}^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} \left({c}^{\mathrm{2}} {l}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} \:=\:\frac{{b}^{\mathrm{2}} {m}^{\mathrm{2}} +{c}^{\mathrm{2}} {l}^{\mathrm{2}} −{lmn}}{\mathrm{4}{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$$\:\:{and}\:\:\boldsymbol{{h}}^{\mathrm{2}} \:=\:\boldsymbol{{p}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} \\ $$$$\:\:{Volume}\:=\:\frac{\boldsymbol{{h}}}{\mathrm{3}}\boldsymbol{{S}}_{{ABC}} \:\:\:\left({may}\:{be}\right). \\ $$
Commented by MrW3 last updated on 05/Nov/18

$${thank}\:{you}\:{for}\:{this}\:{method},\:{sir}.\:{it} \\ $$$${shows}\:{how}\:{to}\:{calculate}\:{the}\:{height}\:{of} \\ $$$${pyramid}. \\ $$
Commented by ajfour last updated on 05/Nov/18

$${Will}\:{this}\:{do}\:{Sir}\:? \\ $$
Commented by ajfour last updated on 05/Nov/18

$${isn}'{t}\:\:\:\:{V}=\frac{{h}}{\mathrm{3}}{S}_{{ABC}} \:\:\:\:{correct}\:? \\ $$
Commented by MrW3 last updated on 05/Nov/18

$${it}\:{is}\:{correct}\:{sir}. \\ $$
