
Question Number 47119 by math solver by abdo. last updated on 05/Nov/18
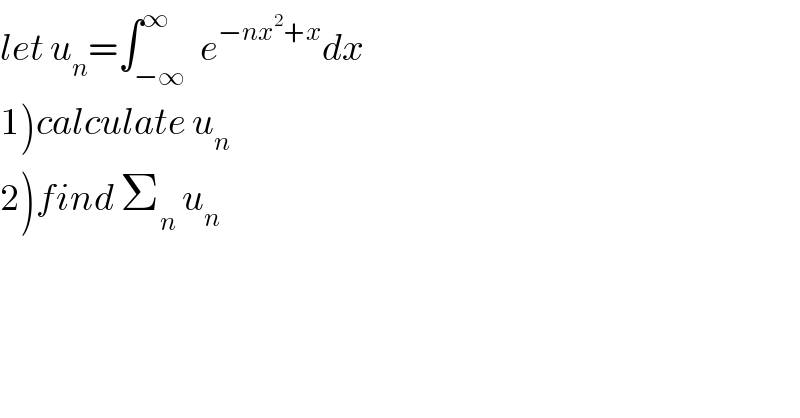
$${let}\:{u}_{{n}} =\int_{−\infty} ^{\infty} \:{e}^{−{nx}^{\mathrm{2}} +{x}} {dx} \\ $$$$\left.\mathrm{1}\right){calculate}\:{u}_{{n}} \\ $$$$\left.\mathrm{2}\right){find}\:\sum_{{n}} \:{u}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 05/Nov/18
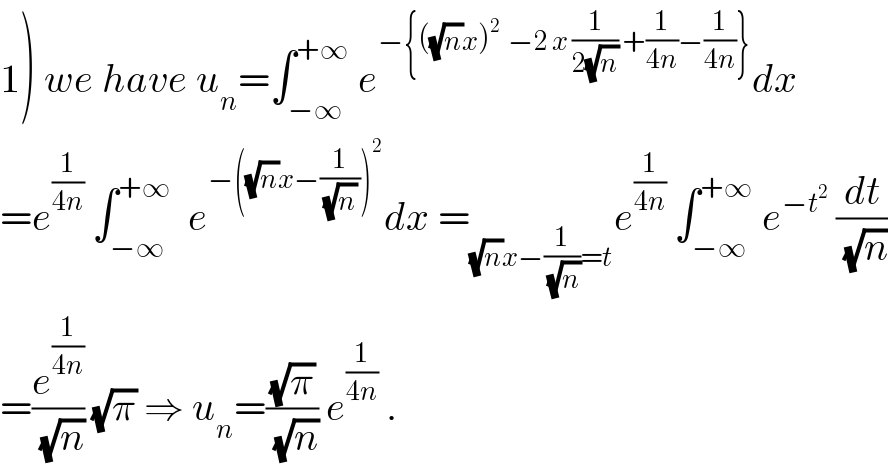
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{u}_{{n}} =\int_{−\infty} ^{+\infty} \:{e}^{−\left\{\left(\sqrt{{n}}{x}\right)^{\mathrm{2}} \:\:−\mathrm{2}\:{x}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\:+\frac{\mathrm{1}}{\mathrm{4}{n}}−\frac{\mathrm{1}}{\mathrm{4}{n}}\right\}} {dx}\: \\ $$$$={e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left(\sqrt{{n}}{x}−\frac{\mathrm{1}}{\sqrt{{n}}\:}\right)^{\mathrm{2}} } {dx}\:=_{\sqrt{{n}}{x}−\frac{\mathrm{1}}{\sqrt{{n}}}={t}} {e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \:\int_{−\infty} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} } \:\frac{{dt}}{\sqrt{{n}}} \\ $$$$=\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} }{\sqrt{{n}}}\:\sqrt{\pi}\:\Rightarrow\:{u}_{{n}} =\frac{\sqrt{\pi}}{\sqrt{{n}}}\:{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \:. \\ $$
