
Question Number 47111 by peter frank last updated on 04/Nov/18

Commented by MrW3 last updated on 04/Nov/18
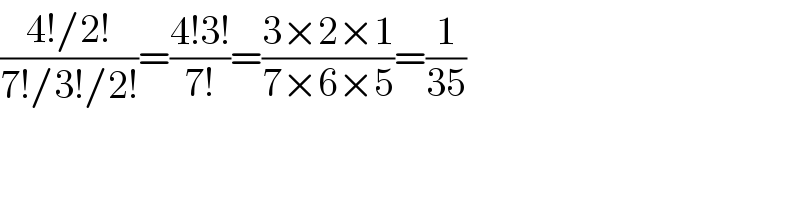
$$\frac{\mathrm{4}!/\mathrm{2}!}{\mathrm{7}!/\mathrm{3}!/\mathrm{2}!}=\frac{\mathrm{4}!\mathrm{3}!}{\mathrm{7}!}=\frac{\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{7}×\mathrm{6}×\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{35}} \\ $$
Commented by peter frank last updated on 05/Nov/18
$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{more}\:\mathrm{explanation} \\ $$
Commented by MrW3 last updated on 05/Nov/18

$${total}\:{number}\:{of}\:{ways}\:{to}\:{arrange}\:\mathrm{7} \\ $$$${letters}\:{is}\:\mathrm{7}!,\:{but}\:{there}\:{are}\:\mathrm{3}\:{letters}\:{M} \\ $$$${and}\:\mathrm{2}\:{letters}\:{I},\:{therefore}\:{the}\:{total} \\ $$$${number}\:{of}\:{different}\:{ways}\:{to}\:{arrange} \\ $$$${the}\:{letters}\:{from}\:{MINIMUM}\:{is} \\ $$$$\frac{\mathrm{7}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{420} \\ $$$${now}\:{we}\:{put}\:{MMM}\:{at}\:{begining}\:{and}\:{arrange} \\ $$$${the}\:{rest}\:\mathrm{4}\:{letters}.\:{to}\:{arrange}\:\mathrm{4}\:{letters} \\ $$$${there}\:{are}\:\mathrm{4}!\:{ways},\:{but}\:\mathrm{2}\:{letters}\:{I}\:{are}\: \\ $$$${identical},\:{so}\:{the}\:{number}\:{of}\:{different} \\ $$$${ways}\:{to}\:{arrange}\:{the}\:\mathrm{4}\:{letters}\:{INIU}\:{is} \\ $$$$\frac{\mathrm{4}!}{\mathrm{2}!}=\mathrm{12} \\ $$$${thus}\:{the}\:{probabilty}\:{that}\:{MMM}\:{begins} \\ $$$${is} \\ $$$$\frac{\frac{\mathrm{4}!}{\mathrm{2}!}}{\frac{\mathrm{7}!}{\mathrm{3}!\mathrm{2}!}}=\frac{\mathrm{12}}{\mathrm{420}}=\left(\frac{\mathrm{4}!\mathrm{3}!}{\mathrm{7}!}=\frac{\mathrm{3}!}{\mathrm{7}×\mathrm{6}×\mathrm{5}}=\frac{\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{7}×\mathrm{6}×\mathrm{5}}\right)=\frac{\mathrm{1}}{\mathrm{35}} \\ $$
Commented by peter frank last updated on 05/Nov/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
