
Question Number 47070 by Meritguide1234 last updated on 04/Nov/18

Commented by maxmathsup by imad last updated on 04/Nov/18
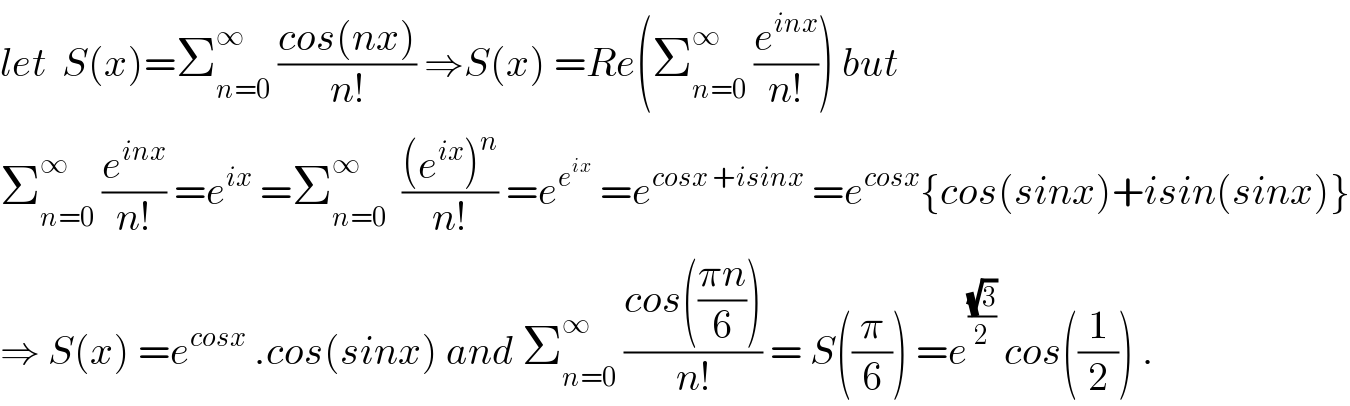
$${let}\:\:{S}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}!}\:\Rightarrow{S}\left({x}\right)\:={Re}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}!}\right)\:{but} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}!}\:={e}^{{ix}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}!}\:={e}^{{e}^{{ix}} } \:={e}^{{cosx}\:+{isinx}} \:={e}^{{cosx}} \left\{{cos}\left({sinx}\right)+{isin}\left({sinx}\right)\right\} \\ $$$$\Rightarrow\:{S}\left({x}\right)\:={e}^{{cosx}} \:.{cos}\left({sinx}\right)\:{and}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{cos}\left(\frac{\pi{n}}{\mathrm{6}}\right)}{{n}!}\:=\:{S}\left(\frac{\pi}{\mathrm{6}}\right)\:={e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:. \\ $$
Commented by Meritguide1234 last updated on 04/Nov/18
$${creative}\:{approach} \\ $$
