
Question Number 47005 by ajfour last updated on 03/Nov/18
Commented by ajfour last updated on 03/Nov/18

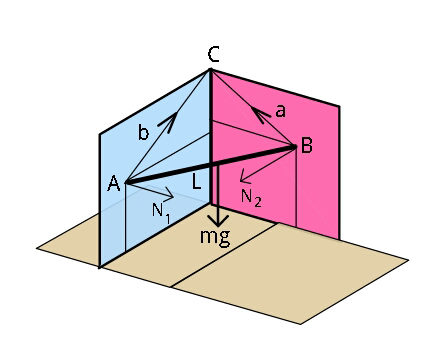
$${A}\:{stick}\:{of}\:{length}\:{L}\:{is}\:{held}\:{balanced} \\ $$$${against}\:{two}\:{mutually}\:{perpendicular} \\ $$$${frictionless}\:{walls},\:{with}\:{the}\:{help} \\ $$$${of}\:{two}\:{strings}\:{AC}\left({length}\:{b}\right)\:{and} \\ $$$${BC}\left({length}\:{a}\right).\:{Find}\:{Tensions} \\ $$$${and}\:{Normal}\:{reactions}\:{T}_{\mathrm{1}} ,\:{T}_{\mathrm{2}} ,\:{N}_{\mathrm{1}} , \\ $$$${and}\:{N}_{\mathrm{2}} .\:\left({mass}\:{of}\:{stick}\:{is}\:{m}\right). \\ $$
Answered by MrW3 last updated on 04/Nov/18
Commented by MrW3 last updated on 04/Nov/18
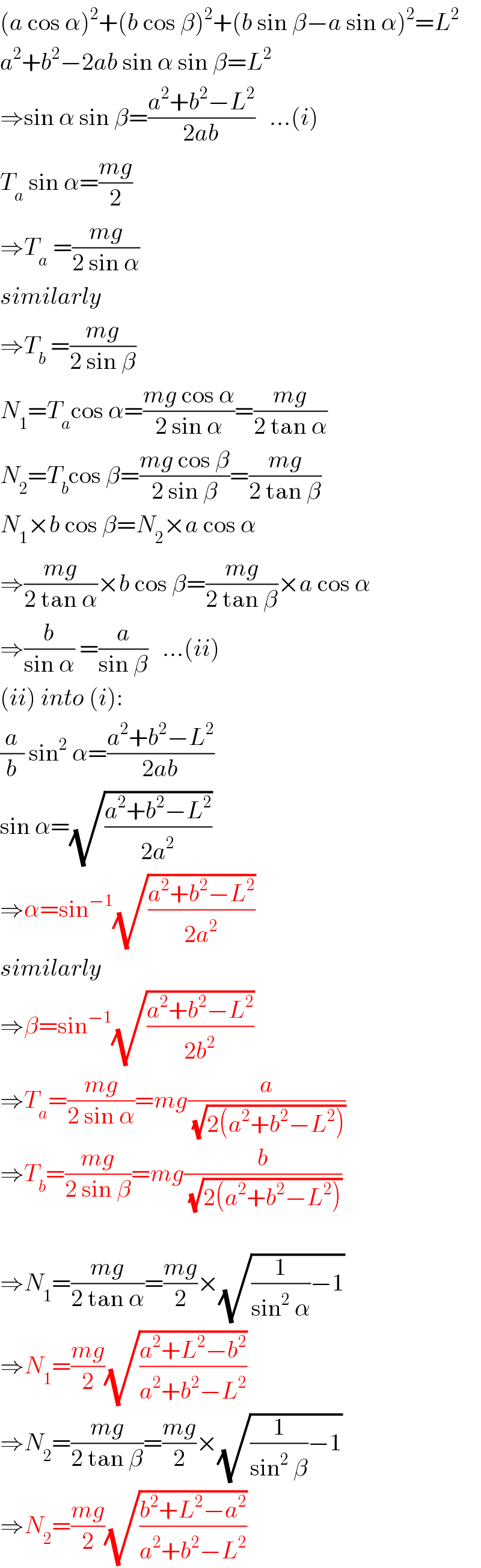
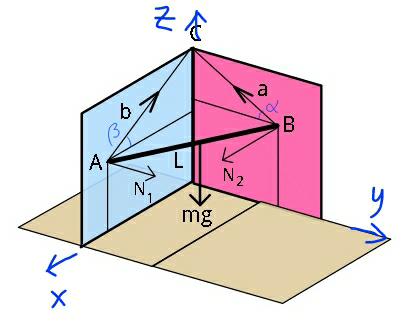
$$\left({a}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left({b}\:\mathrm{cos}\:\beta\right)^{\mathrm{2}} +\left({b}\:\mathrm{sin}\:\beta−{a}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} ={L}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta={L}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }{\mathrm{2}{ab}}\:\:\:...\left({i}\right) \\ $$$${T}_{{a}} \:\mathrm{sin}\:\alpha=\frac{{mg}}{\mathrm{2}} \\ $$$$\Rightarrow{T}_{{a}} \:=\frac{{mg}}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$${similarly} \\ $$$$\Rightarrow{T}_{{b}} \:=\frac{{mg}}{\mathrm{2}\:\mathrm{sin}\:\beta} \\ $$$${N}_{\mathrm{1}} ={T}_{{a}} \mathrm{cos}\:\alpha=\frac{{mg}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{sin}\:\alpha}=\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\alpha} \\ $$$${N}_{\mathrm{2}} ={T}_{{b}} \mathrm{cos}\:\beta=\frac{{mg}\:\mathrm{cos}\:\beta}{\mathrm{2}\:\mathrm{sin}\:\beta}=\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\beta} \\ $$$${N}_{\mathrm{1}} ×{b}\:\mathrm{cos}\:\beta={N}_{\mathrm{2}} ×{a}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\alpha}×{b}\:\mathrm{cos}\:\beta=\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\beta}×{a}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\frac{{b}}{\mathrm{sin}\:\alpha}\:=\frac{{a}}{\mathrm{sin}\:\beta}\:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)\:{into}\:\left({i}\right): \\ $$$$\frac{{a}}{{b}}\:\mathrm{sin}^{\mathrm{2}} \:\alpha=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\mathrm{sin}\:\alpha=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }{\mathrm{2}{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} \sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }{\mathrm{2}{a}^{\mathrm{2}} }} \\ $$$${similarly} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }{\mathrm{2}{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow{T}_{{a}} =\frac{{mg}}{\mathrm{2}\:\mathrm{sin}\:\alpha}={mg}\frac{{a}}{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} \right)}} \\ $$$$\Rightarrow{T}_{{b}} =\frac{{mg}}{\mathrm{2}\:\mathrm{sin}\:\beta}={mg}\frac{{b}}{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} \right)}} \\ $$$$ \\ $$$$\Rightarrow{N}_{\mathrm{1}} =\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\alpha}=\frac{{mg}}{\mathrm{2}}×\sqrt{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\alpha}−\mathrm{1}} \\ $$$$\Rightarrow{N}_{\mathrm{1}} =\frac{{mg}}{\mathrm{2}}\sqrt{\frac{{a}^{\mathrm{2}} +{L}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }} \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\beta}=\frac{{mg}}{\mathrm{2}}×\sqrt{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\beta}−\mathrm{1}} \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\frac{{mg}}{\mathrm{2}}\sqrt{\frac{{b}^{\mathrm{2}} +{L}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{L}^{\mathrm{2}} }} \\ $$
