
Question Number 46935 by ajfour last updated on 02/Nov/18
Commented by ajfour last updated on 03/Nov/18
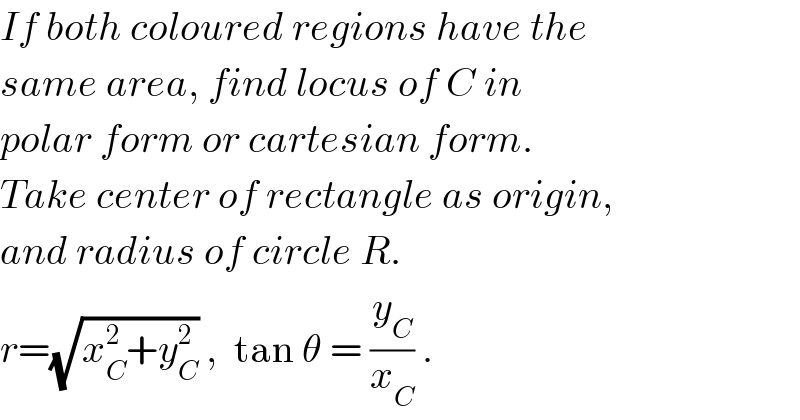
$${If}\:{both}\:{coloured}\:{regions}\:{have}\:{the} \\ $$$${same}\:{area},\:{find}\:{locus}\:{of}\:{C}\:{in} \\ $$$${polar}\:{form}\:{or}\:{cartesian}\:{form}. \\ $$$${Take}\:{center}\:{of}\:{rectangle}\:{as}\:{origin}, \\ $$$${and}\:{radius}\:{of}\:{circle}\:{R}. \\ $$$${r}=\sqrt{{x}_{{C}} ^{\mathrm{2}} +{y}_{{C}} ^{\mathrm{2}} }\:,\:\:\mathrm{tan}\:\theta\:=\:\frac{{y}_{{C}} }{{x}_{{C}} }\:. \\ $$
Answered by ajfour last updated on 04/Nov/18

$${let}\:{center}\:{of}\:{circle}\:{be}\:{origin}. \\ $$$${Eq}.\:{is}\:\:\:{x}={R}\mathrm{cos}\:\phi\:;\:{y}\:=\:{R}\mathrm{sin}\:\phi \\ $$$${center}\:{of}\:{rectangle}\:\left(−{r}\mathrm{cos}\:\theta,\:−{r}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\phi=\:\pi+\theta\:\:\:\:\:\:\:\:\:...\left({i}\right) \\ $$$${upper}\:{edge}:\:\:{y}=−{r}\mathrm{sin}\:\theta+\frac{{b}}{\mathrm{2}} \\ $$$${right}\:{vertical}\:{edge}: \\ $$$$\:\:\:\:{x}=\frac{{a}}{\mathrm{2}}−{r}\mathrm{cos}\:\theta \\ $$$${Let}\:{points}\:{of}\:{intersection}\:{be} \\ $$$${A}\left({left}\right)\:,\:{B}\left({right}\right). \\ $$$$\Rightarrow\:{R}\mathrm{sin}\:\phi_{{A}} =−{r}\mathrm{sin}\:\theta_{{A}} +\frac{{b}}{\mathrm{2}} \\ $$$${using}\:\left({i}\right) \\ $$$$\Rightarrow\:\:\:{R}\mathrm{sin}\:\theta_{{A}} \:=\:{r}\mathrm{sin}\:\theta_{{A}} −\frac{{b}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta_{{A}} =\frac{{b}}{\mathrm{2}\left({r}−{R}\right)} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${R}\mathrm{cos}\:\phi_{{B}} =\frac{{a}}{\mathrm{2}}−{r}\mathrm{cos}\:\theta_{{B}} \\ $$$$\Rightarrow\:{R}\mathrm{cos}\:\theta_{{B}} =\:{r}\mathrm{cos}\:\theta_{{B}} −\frac{{a}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta_{{B}} =\:\frac{{a}}{\mathrm{2}\left({r}−{R}\right)} \\ $$$$.... \\ $$
