
Question Number 46844 by maxmathsup by imad last updated on 01/Nov/18
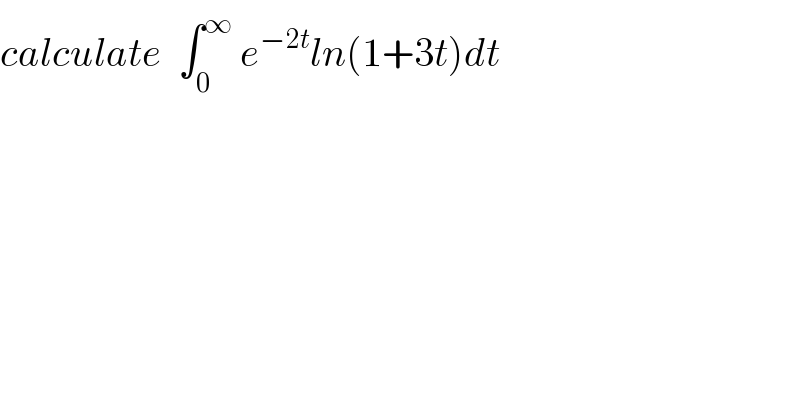
$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}+\mathrm{3}{t}\right){dt}\: \\ $$
Commented by maxmathsup by imad last updated on 04/Nov/18
![let A =∫_0 ^∞ e^(−2t) ln(1+3t)dt changement 1+3t =x give t=((x−1)/3) ⇒ A =∫_1 ^(+∞) e^(−2((x−1)/3)) ln(x)(dx/3) =(1/3) e^(2/(3 )) ∫_1 ^(+∞) e^((−2x)/3) ln(x)dx let find for λ>0 W_λ =∫_1 ^(+∞) e^(−λx) ln(x)dx by parts W_λ =[−(1/λ)e^(−λx) ln(x)]_1 ^(+∞) +(1/λ)∫_1 ^(+∞) e^(−λx) (dx/x) =(1/λ) ∫_1 ^(+∞) e^(−(λ+1)x) dx =(1/λ)[−(1/(λ+1)) e^(−(λ+1)x) ]_1 ^(+∞) =((−1)/(λ(λ+1)))(−e^(−(λ+1)) ) =(e^(−λ−1) /(λ(λ+1))) ⇒∫_1 ^(+∞) e^((−2x)/3) lnx)dx = (e^(−(2/3)−1) /((2/3)((2/3)+1))) =(3/2) .(3/5) e^(−(5/3)) =(9/(10)) e^(−(5/3)) ⇒ A =(1/3) e^(2/3) (9/(10)) e^(−(5/3)) = (3/(10)) e^(−1) =(3/(10e)) .](Q47118.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}+\mathrm{3}{t}\right){dt}\:{changement}\:\mathrm{1}+\mathrm{3}{t}\:={x}\:{give}\:{t}=\frac{{x}−\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$${A}\:=\int_{\mathrm{1}} ^{+\infty} \:{e}^{−\mathrm{2}\frac{{x}−\mathrm{1}}{\mathrm{3}}} {ln}\left({x}\right)\frac{{dx}}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{\frac{\mathrm{2}}{\mathrm{3}\:}} \:\int_{\mathrm{1}} ^{+\infty} \:{e}^{\frac{−\mathrm{2}{x}}{\mathrm{3}}} \:{ln}\left({x}\right){dx}\:{let}\:{find}\:{for}\:\lambda>\mathrm{0} \\ $$$${W}_{\lambda} =\int_{\mathrm{1}} ^{+\infty} \:{e}^{−\lambda{x}} {ln}\left({x}\right){dx}\:{by}\:{parts}\:{W}_{\lambda} =\left[−\frac{\mathrm{1}}{\lambda}{e}^{−\lambda{x}} {ln}\left({x}\right)\right]_{\mathrm{1}} ^{+\infty} \:+\frac{\mathrm{1}}{\lambda}\int_{\mathrm{1}} ^{+\infty} \:{e}^{−\lambda{x}} \frac{{dx}}{{x}} \\ $$$$=\frac{\mathrm{1}}{\lambda}\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−\left(\lambda+\mathrm{1}\right){x}} {dx}\:=\frac{\mathrm{1}}{\lambda}\left[−\frac{\mathrm{1}}{\lambda+\mathrm{1}}\:{e}^{−\left(\lambda+\mathrm{1}\right){x}} \right]_{\mathrm{1}} ^{+\infty} =\frac{−\mathrm{1}}{\lambda\left(\lambda+\mathrm{1}\right)}\left(−{e}^{−\left(\lambda+\mathrm{1}\right)} \right) \\ $$$$\left.=\frac{{e}^{−\lambda−\mathrm{1}} }{\lambda\left(\lambda+\mathrm{1}\right)}\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \:{e}^{\frac{−\mathrm{2}{x}}{\mathrm{3}}} {lnx}\right){dx}\:=\:\frac{{e}^{−\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} }{\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{1}\right)}\:=\frac{\mathrm{3}}{\mathrm{2}}\:.\frac{\mathrm{3}}{\mathrm{5}}\:{e}^{−\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}\:{e}^{−\frac{\mathrm{5}}{\mathrm{3}}} \:\Rightarrow\:{A}\:=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\frac{\mathrm{9}}{\mathrm{10}}\:{e}^{−\frac{\mathrm{5}}{\mathrm{3}}} \:=\:\frac{\mathrm{3}}{\mathrm{10}}\:{e}^{−\mathrm{1}} \:=\frac{\mathrm{3}}{\mathrm{10}{e}}\:. \\ $$
