
Question Number 4683 by thachan last updated on 21/Feb/16
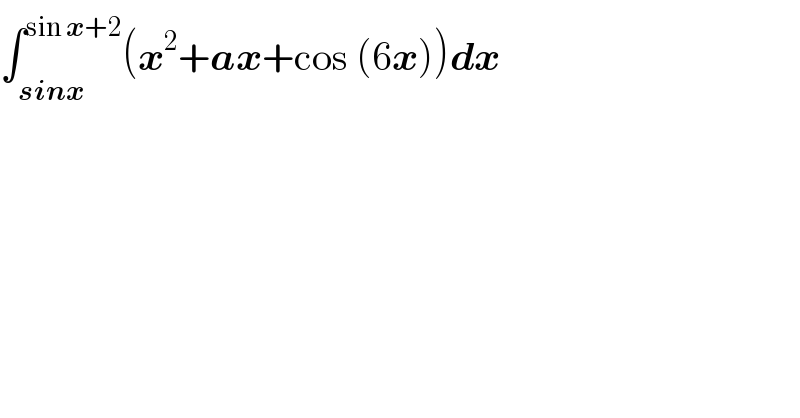
$$\int_{\boldsymbol{{sinx}}} ^{\mathrm{sin}\:\boldsymbol{{x}}+\mathrm{2}} \left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}+\mathrm{cos}\:\left(\mathrm{6}\boldsymbol{{x}}\right)\right)\boldsymbol{{dx}} \\ $$
Commented by prakash jain last updated on 21/Feb/16
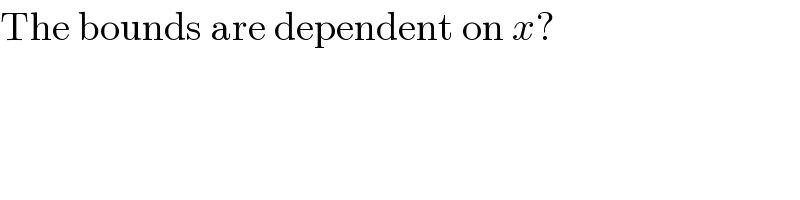
$$\mathrm{The}\:\mathrm{bounds}\:\mathrm{are}\:\mathrm{dependent}\:\mathrm{on}\:{x}? \\ $$
Commented by thachan last updated on 21/Feb/16

$${yex}.{it}\:{are} \\ $$
Commented by thachan last updated on 22/Feb/16

$${yex}.{they}\:{are} \\ $$
Commented by Yozzii last updated on 27/Feb/16
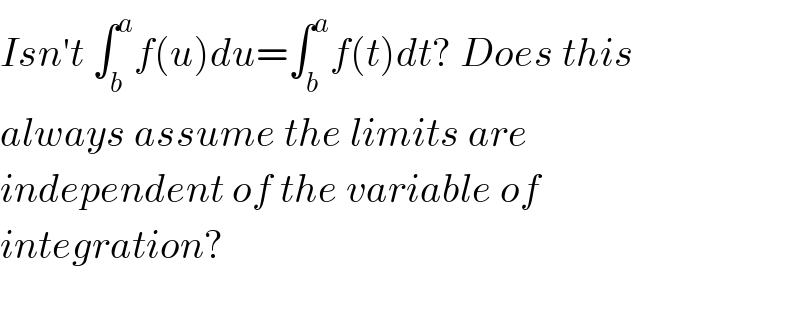
$${Isn}'{t}\:\int_{{b}} ^{{a}} {f}\left({u}\right){du}=\int_{{b}} ^{{a}} {f}\left({t}\right){dt}?\:{Does}\:{this} \\ $$$${always}\:{assume}\:{the}\:{limits}\:{are}\: \\ $$$${independent}\:{of}\:{the}\:{variable}\:{of} \\ $$$${integration}? \\ $$$$ \\ $$
Commented by 123456 last updated on 27/Feb/16
![∫_(sin x) ^(sin x+2) x^2 dx=[(x^3 /3)]_(sin x) ^(sin x+2) =(((sin x+2)^3 −sin^3 x)/3)](Q4711.png)
$$\underset{\mathrm{sin}\:{x}} {\overset{\mathrm{sin}\:{x}+\mathrm{2}} {\int}}{x}^{\mathrm{2}} {dx}=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{sin}\:{x}} ^{\mathrm{sin}\:{x}+\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{sin}\:{x}+\mathrm{2}\right)^{\mathrm{3}} −\mathrm{sin}^{\mathrm{3}} {x}}{\mathrm{3}} \\ $$
Answered by thachan last updated on 21/Feb/16

