
Question Number 4681 by thachan last updated on 21/Feb/16
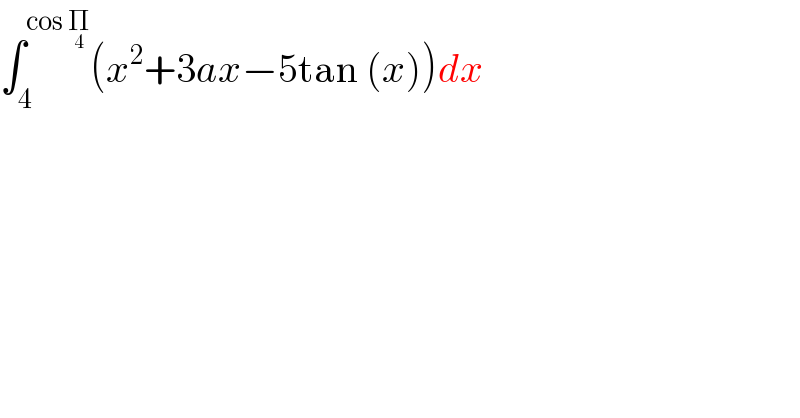
$$\int_{\mathrm{4}} ^{\mathrm{cos}\:\underset{\mathrm{4}} {\prod}} \left({x}^{\mathrm{2}} +\mathrm{3}{ax}−\mathrm{5tan}\:\left({x}\right)\right){dx} \\ $$
Commented by prakash jain last updated on 21/Feb/16
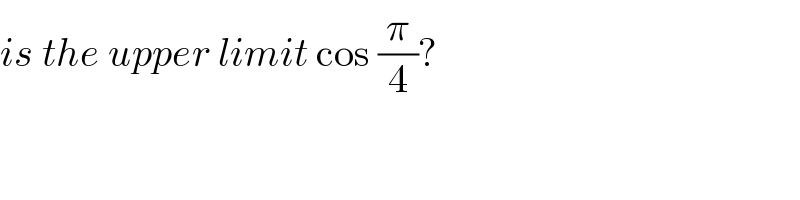
$${is}\:{the}\:{upper}\:{limit}\:\mathrm{cos}\:\frac{\pi}{\mathrm{4}}? \\ $$
Commented by thachan last updated on 21/Feb/16

$${yes}.{it}\:{is}\:{cos} \\ $$
Answered by FilupSmith last updated on 22/Feb/16
![=∫_4 ^( cos(π/4)) x^2 dx+3a∫_4 ^( cos(π/4)) xdx+5∫_4 ^( cos(π/4)) tan(x)dx =(1/3)[(1/(2(√2)))−4^3 ]+(3/2)a[(1/2)−16]+5[ln(cos(4))−ln(cos((1/(√2))))] =(((3−96)a)/4)−((63)/(6(√2)))+5ln(((cos 4)/(cos 2^(−0.5) ))) =((252−558a(√2))/(24(√2)))+5ln(((cos 4)/(cos 2^(−0.5) ))) continue from here](Q4693.png)
$$=\int_{\mathrm{4}} ^{\:\mathrm{cos}\left(\pi/\mathrm{4}\right)} {x}^{\mathrm{2}} {dx}+\mathrm{3}{a}\int_{\mathrm{4}} ^{\:\mathrm{cos}\left(\pi/\mathrm{4}\right)} {xdx}+\mathrm{5}\int_{\mathrm{4}} ^{\:\mathrm{cos}\left(\pi/\mathrm{4}\right)} \mathrm{tan}\left({x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}−\mathrm{4}^{\mathrm{3}} \right]+\frac{\mathrm{3}}{\mathrm{2}}{a}\left[\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{16}\right]+\mathrm{5}\left[\mathrm{ln}\left(\mathrm{cos}\left(\mathrm{4}\right)\right)−\mathrm{ln}\left(\mathrm{cos}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\right)\right] \\ $$$$=\frac{\left(\mathrm{3}−\mathrm{96}\right){a}}{\mathrm{4}}−\frac{\mathrm{63}}{\mathrm{6}\sqrt{\mathrm{2}}}+\mathrm{5ln}\left(\frac{\mathrm{cos}\:\mathrm{4}}{\mathrm{cos}\:\mathrm{2}^{−\mathrm{0}.\mathrm{5}} }\right) \\ $$$$=\frac{\mathrm{252}−\mathrm{558}{a}\sqrt{\mathrm{2}}}{\mathrm{24}\sqrt{\mathrm{2}}}+\mathrm{5ln}\left(\frac{\mathrm{cos}\:\mathrm{4}}{\mathrm{cos}\:\mathrm{2}^{−\mathrm{0}.\mathrm{5}} }\right) \\ $$$$\mathrm{continue}\:\mathrm{from}\:\mathrm{here} \\ $$
