
Question Number 4679 by 314159 last updated on 22/Feb/16
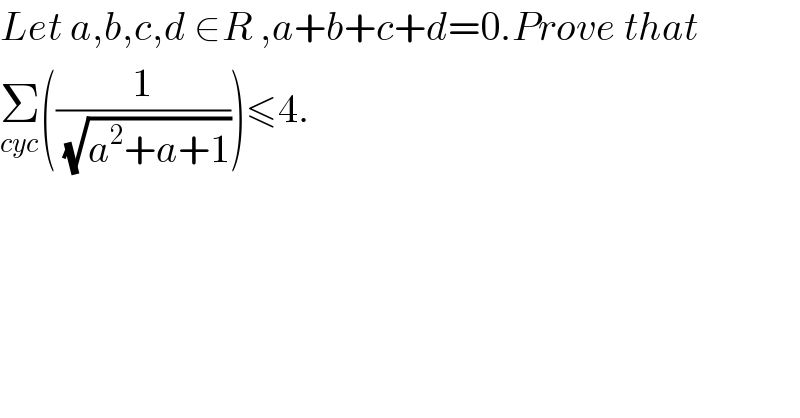
$${Let}\:{a},{b},{c},{d}\:\in{R}\:,{a}+{b}+{c}+{d}=\mathrm{0}.{Prove}\:{that} \\ $$$$\underset{{cyc}} {\sum}\left(\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{a}+\mathrm{1}}}\right)\leqslant\mathrm{4}. \\ $$
Commented by prakash jain last updated on 21/Feb/16
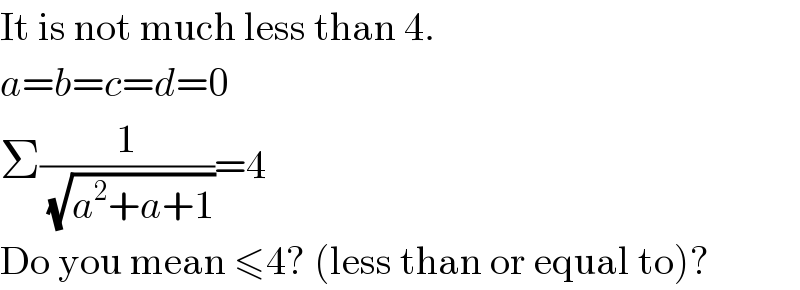
$$\mathrm{It}\:\mathrm{is}\:\mathrm{not}\:\mathrm{much}\:\mathrm{less}\:\mathrm{than}\:\mathrm{4}. \\ $$$${a}={b}={c}={d}=\mathrm{0} \\ $$$$\Sigma\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} +{a}+\mathrm{1}}}=\mathrm{4} \\ $$$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\leqslant\mathrm{4}?\:\left(\mathrm{less}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal}\:\mathrm{to}\right)? \\ $$
Commented by 314159 last updated on 22/Feb/16
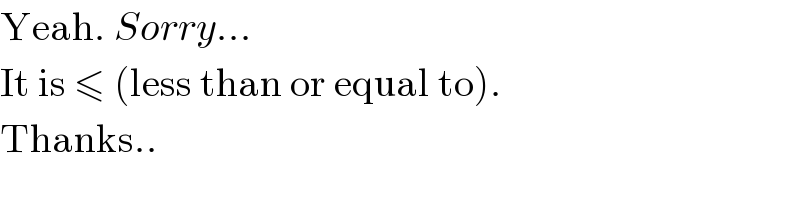
$$\mathrm{Yeah}.\:{Sorry}... \\ $$$$\mathrm{It}\:\mathrm{is}\:\leqslant\:\left(\mathrm{less}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal}\:\mathrm{to}\right). \\ $$$$\mathrm{Thanks}.. \\ $$
