
Question Number 46737 by peter frank last updated on 30/Oct/18

Answered by tanmay.chaudhury50@gmail.com last updated on 31/Oct/18
![Q(asinθ_1 ,bcosθ_1 ) R(asinθ_2 ,bcosθ_2 ) mid point QR is P P=((a(sinθ_1 +sinθ_2 ))/2),((b(cosθ_1 +cosθ_2 ))/2) ={a.sin(((θ_1 +θ_2 )/2))cos(((θ_1 −θ_2 )/2)) ,bcos(((θ_1 +θ_2 )/2))cos(((θ_1 −θ_2 )/2)} α=asin(((θ_1 +θ_2 )/2))cos(((θ_1 −θ_2 )/2)) β=bcos(((θ_1 +θ_2 )/2))cos(((θ_1 −θ_2 )/2)) (∝/β)=(a/b)tan(((θ_1 +θ_2 )/2)) now the eqn of st line ((y−bcosθ_1 )/(b(cosθ_2 −cosθ_1 )))=((x−asinθ_1 )/(a(sinθ_2 −sinθ_1 ))) gradient m=((b(cosθ_2 −cosθ_1 ))/(a(sinθ_2 −sinθ_1 )))=(b/a)×((2sin(((θ_1 +θ_2 )/2))sin(((θ_1 −θ_2 )/2)))/(2cos(((θ_1 +θ_2 )/2))sin(((θ_2 −θ_1 )/2)))) m=−(b/a)×tan(((θ_1 +θ_2 )/2)) tan(((θ_1 +θ_2 )/2))=((−ma)/b) [m=constant gradient] it is already derived (α/β)=(a/b)tan(((θ_1 +θ_2 )/2)) (α/β)=(a/b)×((−ma)/b) so locus is (x/y)=((−ma^2 )/b^2 ) ((b^2 x)/(a^2 y))+m=0 [](Q46750.png)
$${Q}\left({asin}\theta_{\mathrm{1}} ,{bcos}\theta_{\mathrm{1}} \right) \\ $$$${R}\left({asin}\theta_{\mathrm{2}} ,{bcos}\theta_{\mathrm{2}} \right) \\ $$$${mid}\:{point}\:{QR}\:{is}\:{P} \\ $$$${P}=\frac{{a}\left({sin}\theta_{\mathrm{1}} +{sin}\theta_{\mathrm{2}} \right)}{\mathrm{2}},\frac{{b}\left({cos}\theta_{\mathrm{1}} +{cos}\theta_{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$=\left\{{a}.{sin}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){cos}\left(\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}}\right)\:,{bcos}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){cos}\left(\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}}\right\}\right. \\ $$$$\alpha={asin}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){cos}\left(\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\beta={bcos}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){cos}\left(\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\frac{\propto}{\beta}=\frac{{a}}{{b}}{tan}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$${now}\:{the}\:{eqn}\:{of}\:{st}\:{line} \\ $$$$\frac{{y}−{bcos}\theta_{\mathrm{1}} }{{b}\left({cos}\theta_{\mathrm{2}} −{cos}\theta_{\mathrm{1}} \right)}=\frac{{x}−{asin}\theta_{\mathrm{1}} }{{a}\left({sin}\theta_{\mathrm{2}} −{sin}\theta_{\mathrm{1}} \right)} \\ $$$${gradient}\:{m}=\frac{{b}\left({cos}\theta_{\mathrm{2}} −{cos}\theta_{\mathrm{1}} \right)}{{a}\left({sin}\theta_{\mathrm{2}} −{sin}\theta_{\mathrm{1}} \right)}=\frac{{b}}{{a}}×\frac{\mathrm{2}{sin}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){sin}\left(\frac{\theta_{\mathrm{1}} −\theta_{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{2}{cos}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right){sin}\left(\frac{\theta_{\mathrm{2}} −\theta_{\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$${m}=−\frac{{b}}{{a}}×{tan}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$${tan}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right)=\frac{−{ma}}{{b}}\:\:\:\:\:\:\left[{m}={constant}\:{gradient}\right] \\ $$$${it}\:{is}\:{already}\:{derived} \\ $$$$\frac{\alpha}{\beta}=\frac{{a}}{{b}}{tan}\left(\frac{\theta_{\mathrm{1}} +\theta_{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\:\:\:\frac{\alpha}{\beta}=\frac{{a}}{{b}}×\frac{−{ma}}{{b}} \\ $$$${so}\:{locus}\:{is} \\ $$$$\frac{{x}}{{y}}=\frac{−{ma}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}}+{m}=\mathrm{0}\:\:\:\left[\right. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 31/Oct/18

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by MrW3 last updated on 31/Oct/18
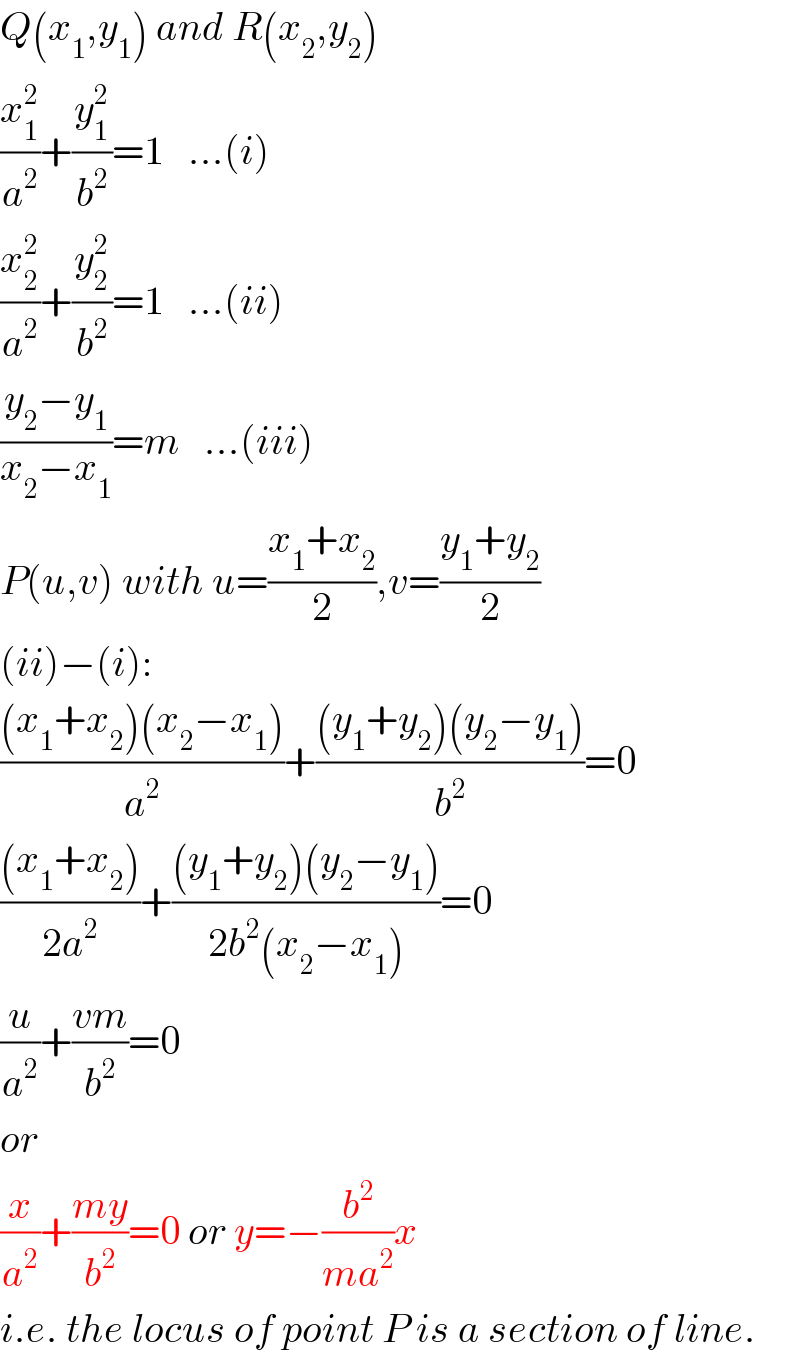
$${Q}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{and}\:{R}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right) \\ $$$$\frac{{x}_{\mathrm{1}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{\mathrm{1}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:...\left({i}\right) \\ $$$$\frac{{x}_{\mathrm{2}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{\mathrm{2}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:...\left({ii}\right) \\ $$$$\frac{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }={m}\:\:\:...\left({iii}\right) \\ $$$${P}\left({u},{v}\right)\:{with}\:{u}=\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}},{v}=\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\frac{\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} }+\frac{\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)}{\mathrm{2}{a}^{\mathrm{2}} }+\frac{\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)}{\mathrm{2}{b}^{\mathrm{2}} \left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)}=\mathrm{0} \\ $$$$\frac{{u}}{{a}^{\mathrm{2}} }+\frac{{vm}}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$${or} \\ $$$$\frac{{x}}{{a}^{\mathrm{2}} }+\frac{{my}}{{b}^{\mathrm{2}} }=\mathrm{0}\:{or}\:{y}=−\frac{{b}^{\mathrm{2}} }{{ma}^{\mathrm{2}} }{x} \\ $$$${i}.{e}.\:{the}\:{locus}\:{of}\:{point}\:{P}\:{is}\:{a}\:{section}\:{of}\:{line}. \\ $$
Commented by peter frank last updated on 31/Oct/18

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
