
Question Number 46713 by agniv last updated on 30/Oct/18
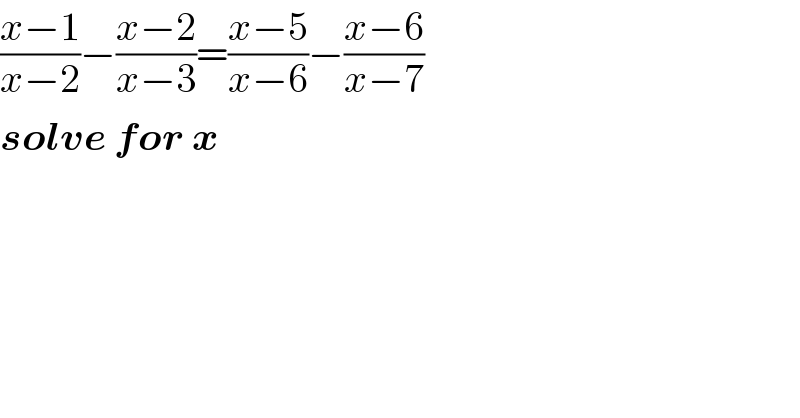
$$\frac{{x}−\mathrm{1}}{{x}−\mathrm{2}}−\frac{{x}−\mathrm{2}}{{x}−\mathrm{3}}=\frac{{x}−\mathrm{5}}{{x}−\mathrm{6}}−\frac{{x}−\mathrm{6}}{{x}−\mathrm{7}} \\ $$$$\boldsymbol{{solve}}\:\boldsymbol{{for}}\:\boldsymbol{{x}} \\ $$
Answered by Kunal12588 last updated on 30/Oct/18
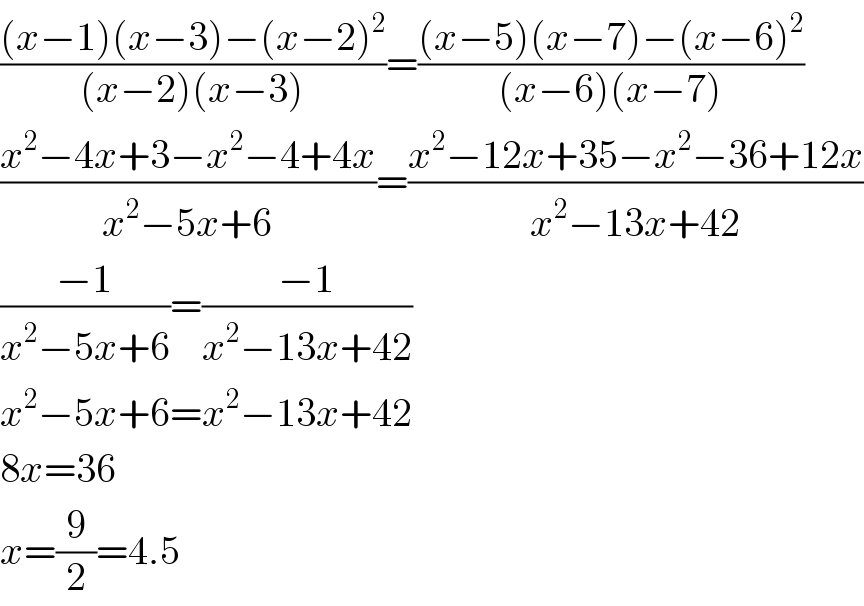
$$\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)−\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)}=\frac{\left({x}−\mathrm{5}\right)\left({x}−\mathrm{7}\right)−\left({x}−\mathrm{6}\right)^{\mathrm{2}} }{\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}−{x}^{\mathrm{2}} −\mathrm{4}+\mathrm{4}{x}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}}=\frac{{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{35}−{x}^{\mathrm{2}} −\mathrm{36}+\mathrm{12}{x}}{{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}} \\ $$$$\frac{−\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}}=\frac{−\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}={x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42} \\ $$$$\mathrm{8}{x}=\mathrm{36} \\ $$$${x}=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
