
Question Number 4671 by 314159 last updated on 20/Feb/16

$${Define}\:{a}\:{function}\:{f}:{R}\rightarrow{R}\:{such}\:{that}\:{f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${for}\:{all}\:{real}\:{x}.{Evaluate}\:{f}\left(\mathrm{0}\right). \\ $$$$ \\ $$
Answered by 123456 last updated on 20/Feb/16
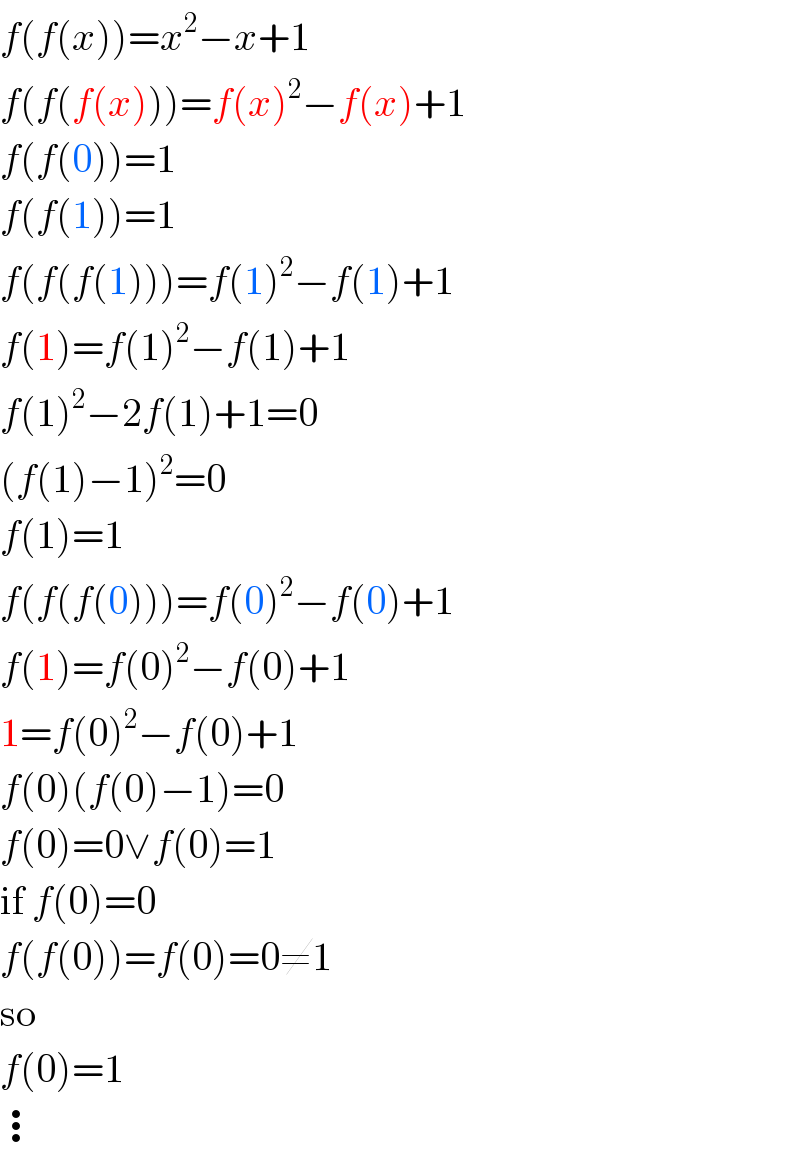
$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)={f}\left({x}\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1} \\ $$$${f}\left({f}\left(\mathrm{1}\right)\right)=\mathrm{1} \\ $$$${f}\left({f}\left({f}\left(\mathrm{1}\right)\right)\right)={f}\left(\mathrm{1}\right)^{\mathrm{2}} −{f}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right)^{\mathrm{2}} −{f}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{f}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\left({f}\left(\mathrm{1}\right)−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left({f}\left({f}\left(\mathrm{0}\right)\right)\right)={f}\left(\mathrm{0}\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)={f}\left(\mathrm{0}\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$$\mathrm{1}={f}\left(\mathrm{0}\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)\left({f}\left(\mathrm{0}\right)−\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\vee{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{if}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)={f}\left(\mathrm{0}\right)=\mathrm{0}\neq\mathrm{1} \\ $$$$\mathrm{so} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\vdots \\ $$
Commented by 123456 last updated on 21/Feb/16
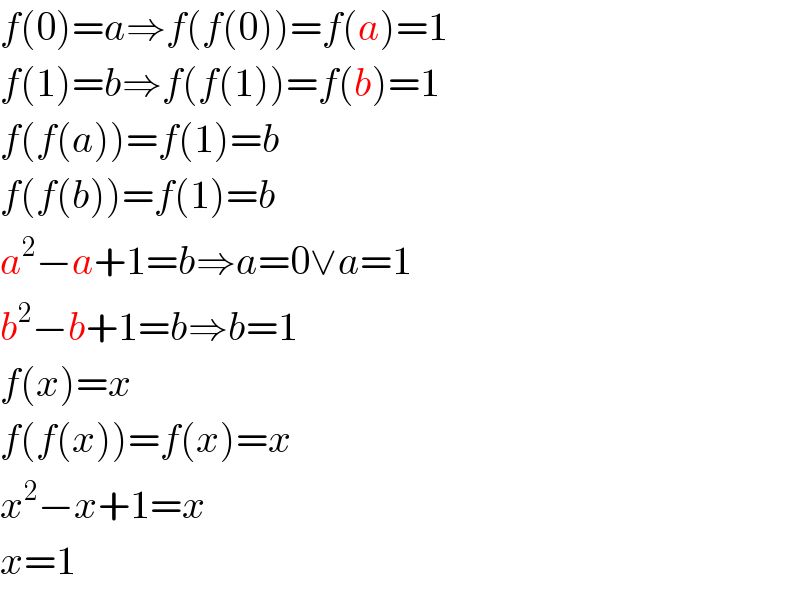
$${f}\left(\mathrm{0}\right)={a}\Rightarrow{f}\left({f}\left(\mathrm{0}\right)\right)={f}\left({a}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)={b}\Rightarrow{f}\left({f}\left(\mathrm{1}\right)\right)={f}\left({b}\right)=\mathrm{1} \\ $$$${f}\left({f}\left({a}\right)\right)={f}\left(\mathrm{1}\right)={b} \\ $$$${f}\left({f}\left({b}\right)\right)={f}\left(\mathrm{1}\right)={b} \\ $$$${a}^{\mathrm{2}} −{a}+\mathrm{1}={b}\Rightarrow{a}=\mathrm{0}\vee{a}=\mathrm{1} \\ $$$${b}^{\mathrm{2}} −{b}+\mathrm{1}={b}\Rightarrow{b}=\mathrm{1} \\ $$$${f}\left({x}\right)={x} \\ $$$${f}\left({f}\left({x}\right)\right)={f}\left({x}\right)={x} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}={x} \\ $$$${x}=\mathrm{1} \\ $$
Commented by 314159 last updated on 21/Feb/16

$${Thanks}\:{a}\:{lot}! \\ $$
