
Previous in Differential Equation Next in Differential Equation
Question Number 46542 by Umar last updated on 28/Oct/18
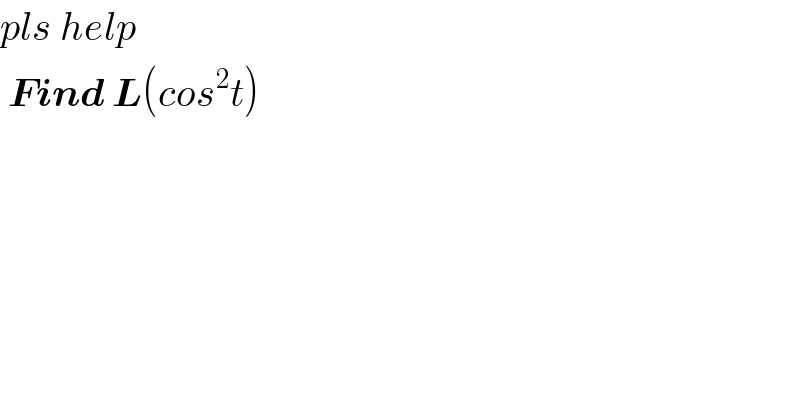
$${pls}\:{help}\: \\ $$$$\:\boldsymbol{{Find}}\:\boldsymbol{{L}}\left({cos}^{\mathrm{2}} {t}\right) \\ $$
Commented by Umar last updated on 28/Oct/18
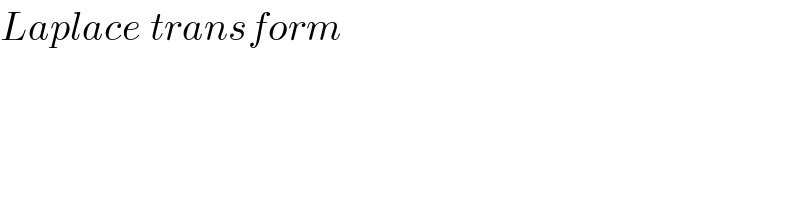
$${Laplace}\:{transform} \\ $$
Commented by maxmathsup by imad last updated on 28/Oct/18
![we have generally L(f(x))=∫_0 ^∞ f(t)e^(−tx) dt ⇒ L(cos^2 x)=∫_0 ^∞ cos^2 t e^(−tx) dt=(1/2)∫_0 ^∞ (1+cos(2t))e^(−tx) dt =(1/2)∫_0 ^∞ e^(−tx) dt +(1/2)∫_0 ^∞ e^(−tx) cos(2t)dt but ∫_0 ^∞ e^(−tx) dt =[−(1/x)e^(−tx) ]_(t=0) ^∞ =(1/x) ∫_0 ^∞ e^(−xt) cos(2t)dt =Re(∫_0 ^∞ e^(−xt+i2t) dt) and ∫_0 ^∞ e^((−x+2i)t) dt =[(1/(−x+2i)) e^((−x+2i)t) ]_(t=0) ^∞ =((−1)/(−x+2i)) =(1/(x−2i)) =((x+2i)/(x^2 +4)) ⇒ ∫_0 ^∞ e^(−xt) cos(2t)dt = (x/(x^2 +4)) ⇒L(cos^2 x)=(1/(2x)) +(x/(2(x^(2 ) +4)))](Q46544.png)
$${we}\:{have}\:{generally}\:{L}\left({f}\left({x}\right)\right)=\int_{\mathrm{0}} ^{\infty} {f}\left({t}\right){e}^{−{tx}} {dt}\:\Rightarrow \\ $$$${L}\left({cos}^{\mathrm{2}} {x}\right)=\int_{\mathrm{0}} ^{\infty} \:{cos}^{\mathrm{2}} {t}\:{e}^{−{tx}} {dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right){e}^{−{tx}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} {dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:{but}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} {dt}\:=\left[−\frac{\mathrm{1}}{{x}}{e}^{−{tx}} \right]_{{t}=\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{{x}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{xt}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}+{i}\mathrm{2}{t}} {dt}\right)\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{x}+\mathrm{2}{i}\right){t}} {dt}\:=\left[\frac{\mathrm{1}}{−{x}+\mathrm{2}{i}}\:{e}^{\left(−{x}+\mathrm{2}{i}\right){t}} \right]_{{t}=\mathrm{0}} ^{\infty} \:=\frac{−\mathrm{1}}{−{x}+\mathrm{2}{i}}\:=\frac{\mathrm{1}}{{x}−\mathrm{2}{i}}\:=\frac{{x}+\mathrm{2}{i}}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:=\:\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow{L}\left({cos}^{\mathrm{2}} {x}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}}\:\:+\frac{{x}}{\mathrm{2}\left({x}^{\mathrm{2}\:} +\mathrm{4}\right)} \\ $$
Commented by maxmathsup by imad last updated on 28/Oct/18
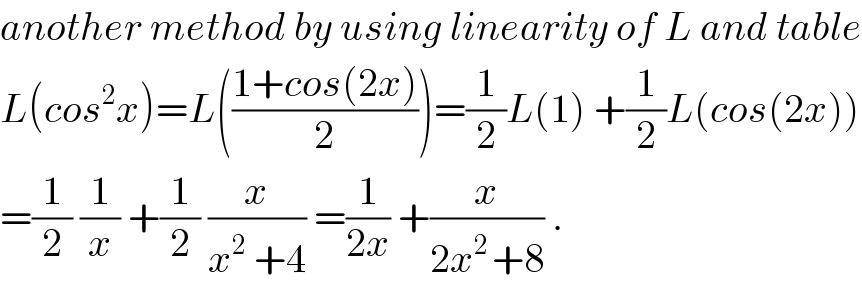
$${another}\:{method}\:{by}\:{using}\:{linearity}\:{of}\:{L}\:{and}\:{table} \\ $$$${L}\left({cos}^{\mathrm{2}} {x}\right)={L}\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{L}\left(\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{L}\left({cos}\left(\mathrm{2}{x}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}{x}}\:+\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}\:} +\mathrm{8}}\:. \\ $$
Commented by Umar last updated on 28/Oct/18

$${thanks} \\ $$
Commented by maxmathsup by imad last updated on 28/Oct/18

$${you}\:{are}\:{welcme}. \\ $$
