
Question Number 45876 by rahul 19 last updated on 17/Oct/18
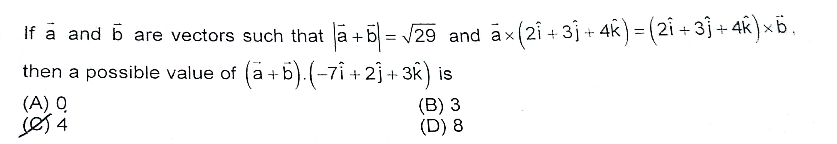
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Oct/18
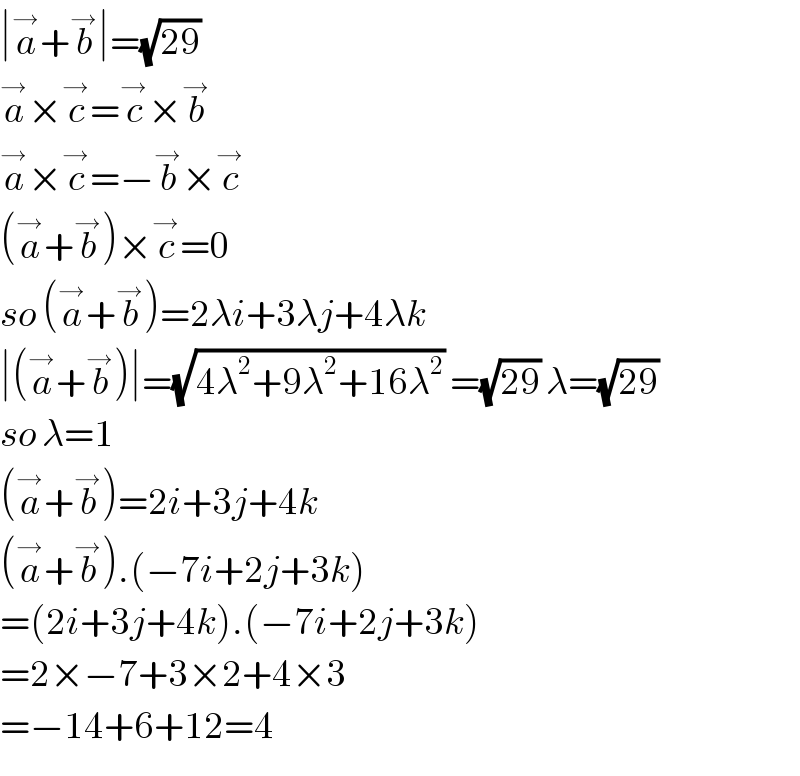
$$\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\mid=\sqrt{\mathrm{29}}\: \\ $$$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{c}}=\overset{\rightarrow} {{c}}×\overset{\rightarrow} {{b}} \\ $$$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{c}}=−\overset{\rightarrow} {{b}}×\overset{\rightarrow} {{c}} \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)×\overset{\rightarrow} {{c}}=\mathrm{0} \\ $$$${so}\:\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)=\mathrm{2}\lambda{i}+\mathrm{3}\lambda{j}+\mathrm{4}\lambda{k} \\ $$$$\mid\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)\mid=\sqrt{\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{9}\lambda^{\mathrm{2}} +\mathrm{16}\lambda^{\mathrm{2}} }\:=\sqrt{\mathrm{29}}\:\lambda=\sqrt{\mathrm{29}}\: \\ $$$${so}\:\lambda=\mathrm{1} \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right)=\mathrm{2}{i}+\mathrm{3}{j}+\mathrm{4}{k} \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}\right).\left(−\mathrm{7}{i}+\mathrm{2}{j}+\mathrm{3}{k}\right) \\ $$$$=\left(\mathrm{2}{i}+\mathrm{3}{j}+\mathrm{4}{k}\right).\left(−\mathrm{7}{i}+\mathrm{2}{j}+\mathrm{3}{k}\right) \\ $$$$=\mathrm{2}×−\mathrm{7}+\mathrm{3}×\mathrm{2}+\mathrm{4}×\mathrm{3} \\ $$$$=−\mathrm{14}+\mathrm{6}+\mathrm{12}=\mathrm{4} \\ $$
Commented by rahul 19 last updated on 18/Oct/18

$${thanks}\:{sir}. \\ $$
