
Question Number 45830 by jashim last updated on 17/Oct/18
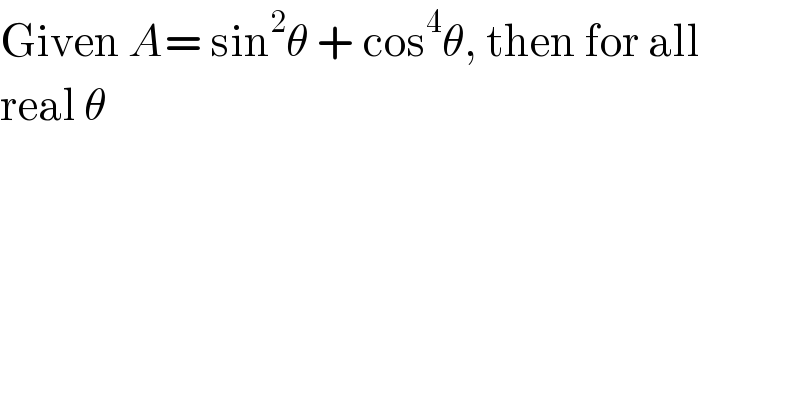
$$\mathrm{Given}\:{A}=\:\mathrm{sin}^{\mathrm{2}} \theta\:+\:\mathrm{cos}^{\mathrm{4}} \theta,\:\mathrm{then}\:\mathrm{for}\:\mathrm{all} \\ $$$$\mathrm{real}\:\theta \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
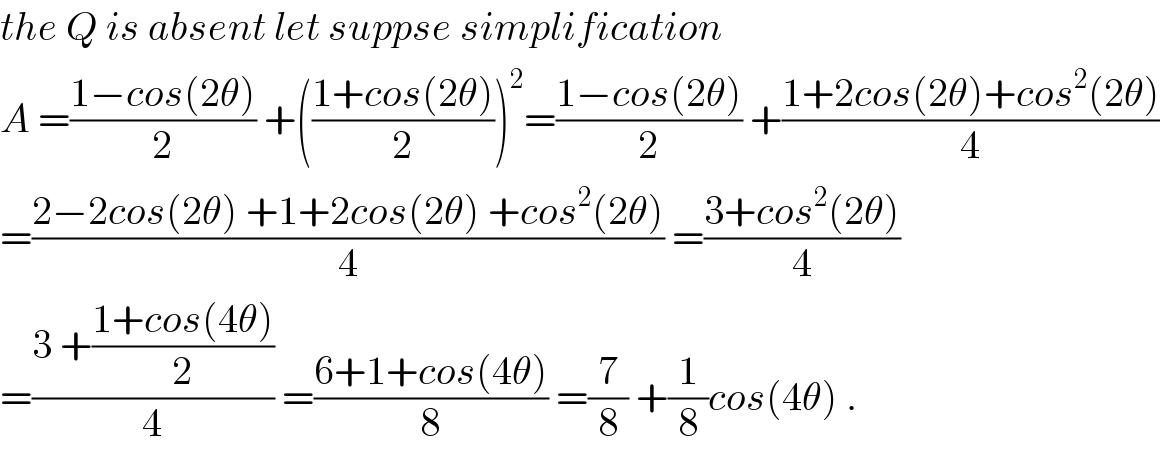
$${the}\:{Q}\:{is}\:{absent}\:{let}\:{suppse}\:{simplification} \\ $$$${A}\:=\frac{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\:+\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\:+\frac{\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)+{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)}{\mathrm{4}} \\ $$$$=\frac{\mathrm{2}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\:+\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)}{\mathrm{4}}\:=\frac{\mathrm{3}+{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}}{\mathrm{4}}\:=\frac{\mathrm{6}+\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{8}}\:=\frac{\mathrm{7}}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{8}}{cos}\left(\mathrm{4}\theta\right)\:. \\ $$
