
Previous in Relation and Functions Next in Relation and Functions
Question Number 45792 by maxmathsup by imad last updated on 16/Oct/18
![let u_n =Σ_(k=1) ^n (((−1)^([k]) )/k) and H_n =Σ_(k=1) ^n (1/k) 1)calculate u_n interms of H_n 2)study the convergence of (u_n ) 3)study theconvergence of Σ u_(n.)](Q45792.png)
$${let}\:{u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{\left[{k}\right]} }{{k}}\:\:{and}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$$$\left.\mathrm{1}\right){calculate}\:{u}_{{n}} \:{interms}\:{of}\:{H}_{{n}} \\ $$$$\left.\mathrm{2}\right){study}\:{the}\:{convergence}\:{of}\:\left({u}_{{n}} \right) \\ $$$$\left.\mathrm{3}\right){study}\:{theconvergence}\:{of}\:\Sigma\:{u}_{{n}.} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
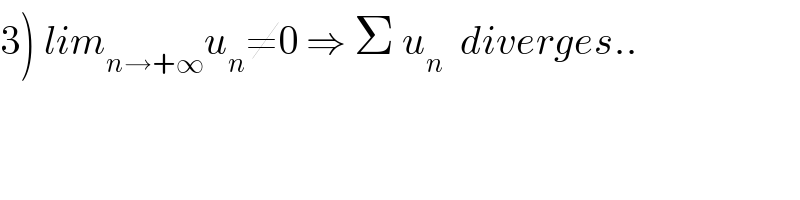
$$\left.\mathrm{3}\right)\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} \neq\mathrm{0}\:\Rightarrow\:\Sigma\:{u}_{{n}} \:\:{diverges}.. \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
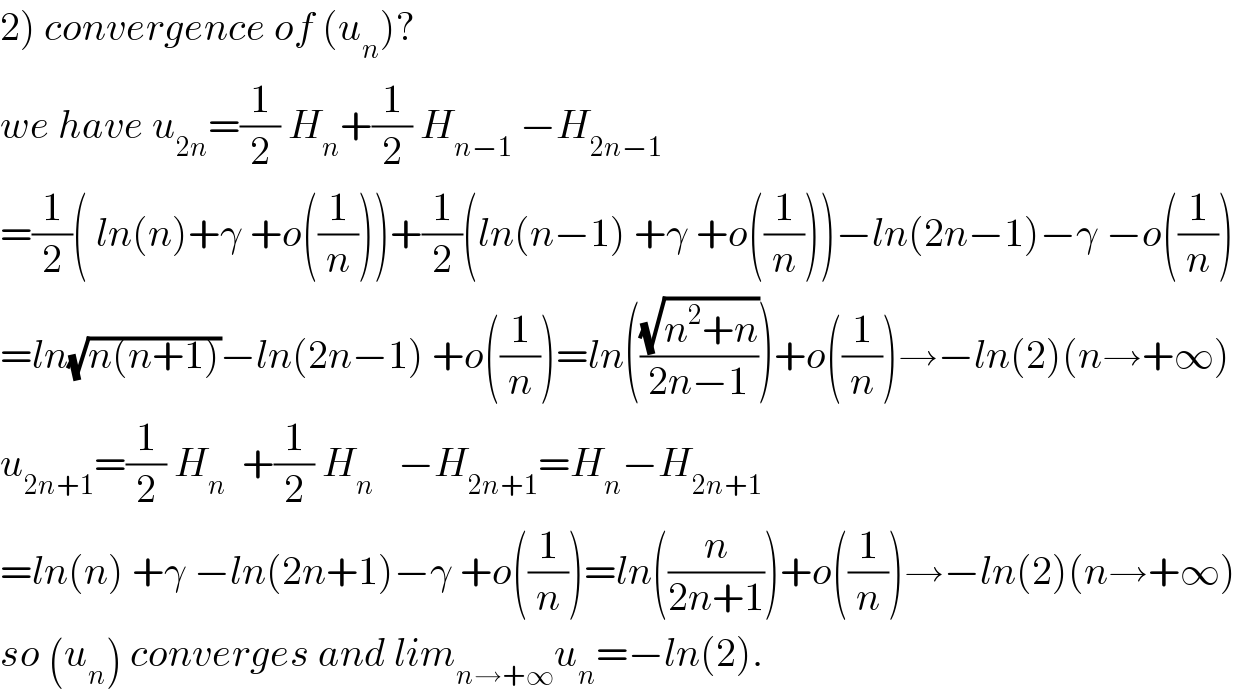
$$\left.\mathrm{2}\right)\:{convergence}\:{of}\:\left({u}_{{n}} \right)? \\ $$$${we}\:{have}\:{u}_{\mathrm{2}{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}−\mathrm{1}} \:−{H}_{\mathrm{2}{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\:{ln}\left({n}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left({n}−\mathrm{1}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)−{ln}\left(\mathrm{2}{n}−\mathrm{1}\right)−\gamma\:−{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$={ln}\sqrt{{n}\left({n}+\mathrm{1}\right)}−{ln}\left(\mathrm{2}{n}−\mathrm{1}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)={ln}\left(\frac{\sqrt{{n}^{\mathrm{2}} +{n}}}{\mathrm{2}{n}−\mathrm{1}}\right)+{o}\left(\frac{\mathrm{1}}{{n}}\right)\rightarrow−{ln}\left(\mathrm{2}\right)\left({n}\rightarrow+\infty\right) \\ $$$${u}_{\mathrm{2}{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:\:\:−{H}_{\mathrm{2}{n}+\mathrm{1}} ={H}_{{n}} −{H}_{\mathrm{2}{n}+\mathrm{1}} \\ $$$$={ln}\left({n}\right)\:+\gamma\:−{ln}\left(\mathrm{2}{n}+\mathrm{1}\right)−\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)={ln}\left(\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}\right)+{o}\left(\frac{\mathrm{1}}{{n}}\right)\rightarrow−{ln}\left(\mathrm{2}\right)\left({n}\rightarrow+\infty\right) \\ $$$${so}\:\left({u}_{{n}} \right)\:{converges}\:{and}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} =−{ln}\left(\mathrm{2}\right). \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
![we have u_n =Σ_(k=1) ^n (((−1)^([k]) )/k) ⇒u_n =Σ_(p=1) ^([(n/2)]) (1/(2p)) −Σ_(p=0) ^([((n−1)/2)]) (1/(2p+1)) but Σ_(p=1) ^([(n/2)]) (1/(2p)) =(1/2) H_([(n/2)]) Σ_(p=0) ^([((n−1)/2)]) (1/(2p+1)) =1 +(1/3) +(1/5) +....+(1/(2[((n−1)/2)]+1)) =1+(1/2) +(1/3) +(1/4) +.....+(1/(2[((n−1)/2)])) +(1/(2[((n−1)/2)]+1)) −(1/2)(1+(1/2) +....+(1/(2[((n−1)/2)]))) =H_(2[((n−1)/2)]+1) −(1/2) H_([((n−1)/2)]) ⇒ u_n =(1/2) H_([(n/2)]) +(1/2) H_([((n−1)/2)]) − H_(2[((n−1)/2)]+1)](Q45872.png)
$${we}\:{have}\:{u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{\left[{k}\right]} }{{k}}\:\Rightarrow{u}_{{n}} =\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{2}{p}}\:−\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}\:{but} \\ $$$$\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{2}{p}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}}{\mathrm{2}}\right]} \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}\:=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+....+\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+.....+\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]}\:+\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+....+\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]}\right) \\ $$$$={H}_{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\:\Rightarrow \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} −\:{H}_{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \\ $$$$ \\ $$
Answered by arcana last updated on 17/Oct/18
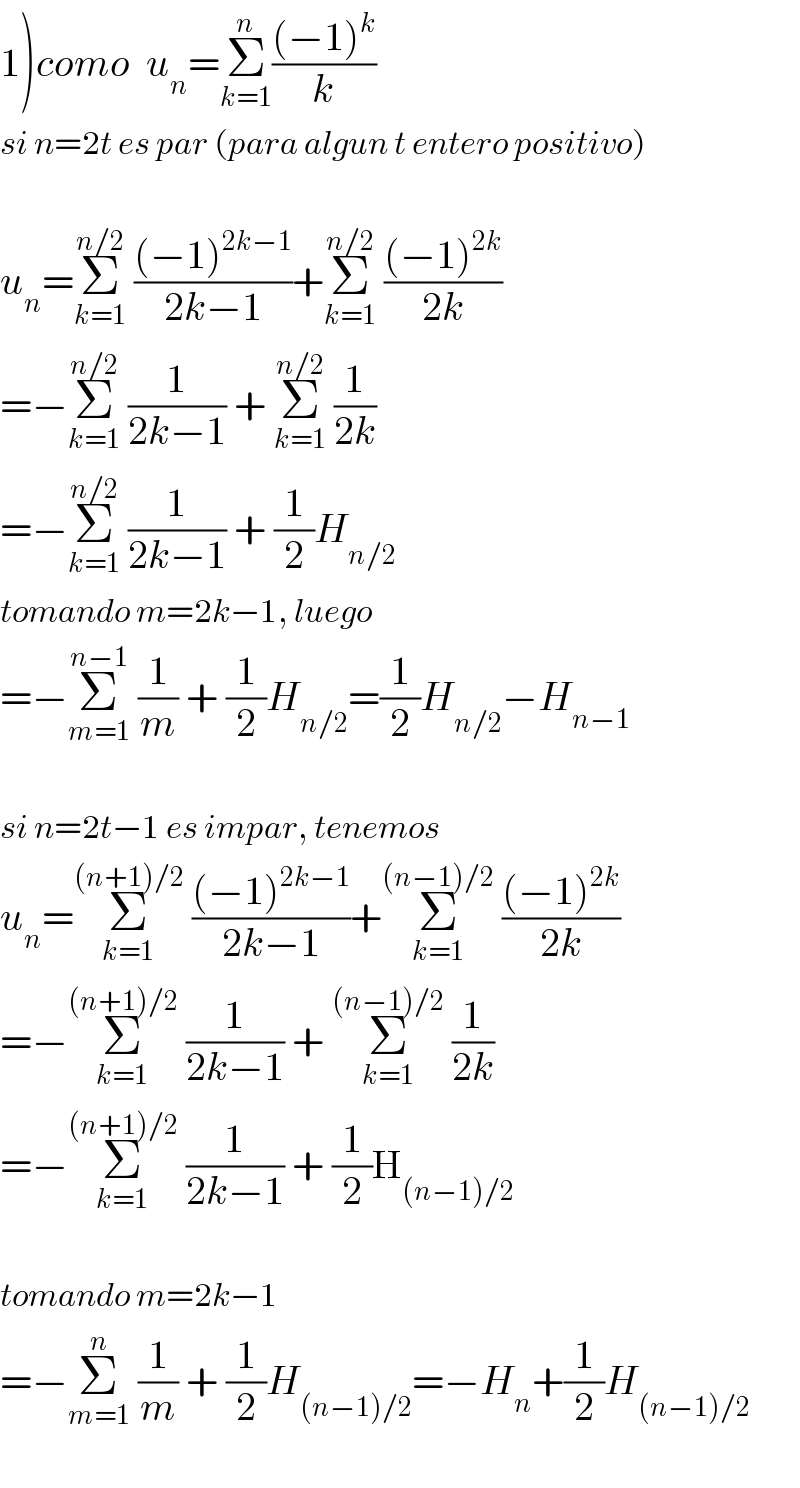
$$\left.\mathrm{1}\right){como}\:\:{u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$${si}\:{n}=\mathrm{2}{t}\:{es}\:{par}\:\left({para}\:{algun}\:{t}\:{entero}\:{positivo}\right) \\ $$$$ \\ $$$${u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{k}−\mathrm{1}} }{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{k}} }{\mathrm{2}{k}} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:+\:\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}/\mathrm{2}} \\ $$$${tomando}\:{m}=\mathrm{2}{k}−\mathrm{1},\:{luego} \\ $$$$=−\underset{{m}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\:\frac{\mathrm{1}}{{m}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}/\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}/\mathrm{2}} −{H}_{{n}−\mathrm{1}} \\ $$$$ \\ $$$${si}\:{n}=\mathrm{2}{t}−\mathrm{1}\:{es}\:{impar},\:{tenemos} \\ $$$${u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{\left({n}+\mathrm{1}\right)/\mathrm{2}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{k}−\mathrm{1}} }{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{\left({n}−\mathrm{1}\right)/\mathrm{2}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{k}} }{\mathrm{2}{k}} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{\left({n}+\mathrm{1}\right)/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:+\:\underset{{k}=\mathrm{1}} {\overset{\left({n}−\mathrm{1}\right)/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{\left({n}+\mathrm{1}\right)/\mathrm{2}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\left({n}−\mathrm{1}\right)/\mathrm{2}} \\ $$$$ \\ $$$${tomando}\:{m}=\mathrm{2}{k}−\mathrm{1} \\ $$$$=−\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{m}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{H}_{\left({n}−\mathrm{1}\right)/\mathrm{2}} =−{H}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}{H}_{\left({n}−\mathrm{1}\right)/\mathrm{2}} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
$${thank}\:{you}\:{Arkana}\:{for}\:{this}\:{work}... \\ $$
Answered by arcana last updated on 17/Oct/18

$$\mathrm{3}.\:{como}\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{x}\right)^{{k}} \:\:{para}\:\mid{x}\mid<\mathrm{1} \\ $$$${integrando}\:{a}\:{ambos}\:{lados}\:{vemos}\:{que} \\ $$$$\Rightarrow{ln}\:\left(\mathrm{1}+{x}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\centerdot{x}^{{k}+\mathrm{1}} \\ $$$${con}\:−\mathrm{1}<{x}\leqslant\mathrm{1}.\:{Si}\:{x}=\mathrm{1},\:{entonces} \\ $$$$ \\ $$$${ln}\left(\mathrm{2}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}=\Sigma{u}_{{n}} \\ $$
