Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140040 by bobhans last updated on 03/May/21

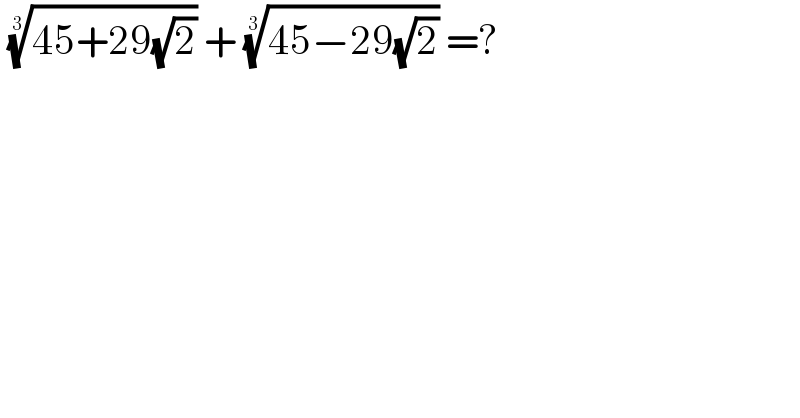
((45+29(√2)))^(1/3) + ((45−29(√2)))^(1/3) =?

$$\:\sqrt[{\mathrm{3}}]{\mathrm{45}+\mathrm{29}\sqrt{\mathrm{2}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{45}−\mathrm{29}\sqrt{\mathrm{2}}}\:=?\: \\ $$

Answered by cherokeesay last updated on 05/May/21

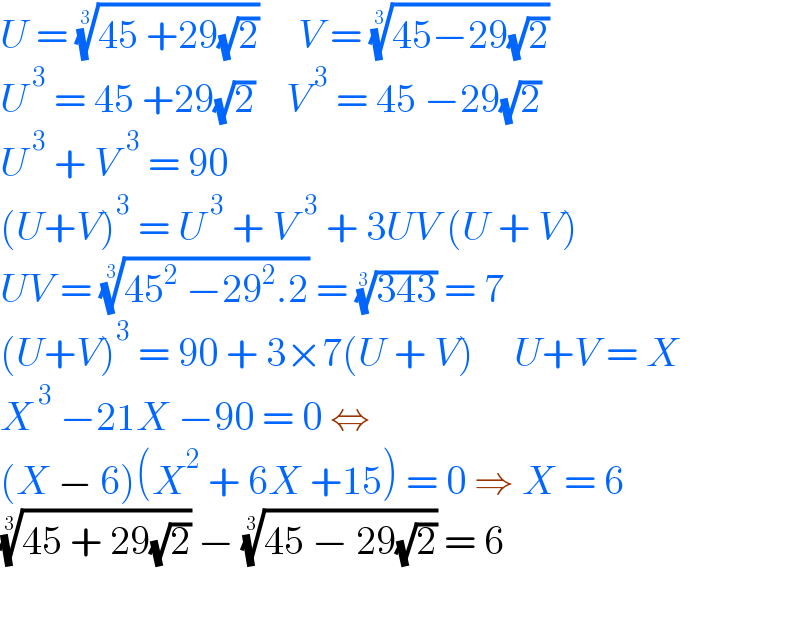
U = ((45 +29(√2)))^(1/3) V = ((45−29(√2)))^(1/3) U^( 3) = 45 +29(√2) V^( 3) = 45 −29(√2) U^( 3) + V^( 3) = 90 (U+V)^3 = U^( 3) + V^( 3) + 3UV (U + V) UV = ((45^2 −29^2 .2))^(1/3) = ((343))^(1/3) = 7 (U+V)^3 = 90 + 3×7(U + V) U+V = X X^( 3) −21X −90 = 0 ⇔ (X − 6)(X^2 + 6X +15) = 0 ⇒ X = 6 ((45 + 29(√2)))^(1/3) − ((45 − 29(√2)))^(1/3) = 6

$${U}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{45}\:+\mathrm{29}\sqrt{\mathrm{2}}}\:\:\:\:\:{V}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{45}−\mathrm{29}\sqrt{\mathrm{2}}} \\ $$$${U}^{\:\mathrm{3}} \:=\:\mathrm{45}\:+\mathrm{29}\sqrt{\mathrm{2}}\:\:\:\:{V}^{\:\mathrm{3}} \:=\:\mathrm{45}\:−\mathrm{29}\sqrt{\mathrm{2}}\:\: \\ $$$${U}^{\:\mathrm{3}} \:+\:{V}^{\:\:\mathrm{3}} \:=\:\mathrm{90} \\ $$$$\left({U}+{V}\right)^{\mathrm{3}} \:=\:{U}^{\:\mathrm{3}} \:+\:{V}^{\:\:\mathrm{3}} \:+\:\mathrm{3}{UV}\:\left({U}\:+\:{V}\right) \\ $$$${UV}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{45}^{\mathrm{2}} \:−\mathrm{29}^{\mathrm{2}} .\mathrm{2}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{343}}\:=\:\mathrm{7} \\ $$$$\left({U}+{V}\right)^{\mathrm{3}} \:=\:\mathrm{90}\:+\:\mathrm{3}×\mathrm{7}\left({U}\:+\:{V}\right)\:\:\:\:\:{U}+{V}\:=\:{X} \\ $$$${X}^{\:\mathrm{3}} \:−\mathrm{21}{X}\:−\mathrm{90}\:=\:\mathrm{0}\:\Leftrightarrow\: \\ $$$$\left({X}\:−\:\mathrm{6}\right)\left({X}^{\mathrm{2}} \:+\:\mathrm{6}{X}\:+\mathrm{15}\right)\:=\:\mathrm{0}\:\Rightarrow\:{X}\:=\:\mathrm{6} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{45}\:+\:\mathrm{29}\sqrt{\mathrm{2}}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{45}\:−\:\mathrm{29}\sqrt{\mathrm{2}}}\:=\:\mathrm{6} \\ $$$$ \\ $$

Answered by abdullahoudou last updated on 03/May/21

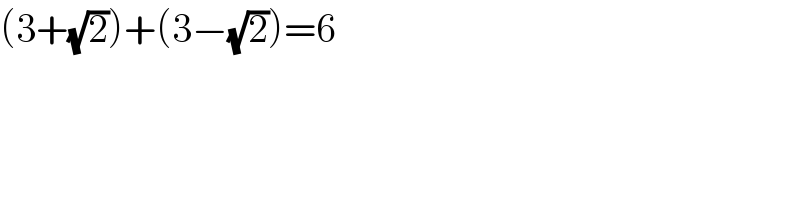
(3+(√2))+(3−(√2))=6

$$\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)+\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)=\mathrm{6} \\ $$$$ \\ $$

Answered by MJS_new last updated on 03/May/21

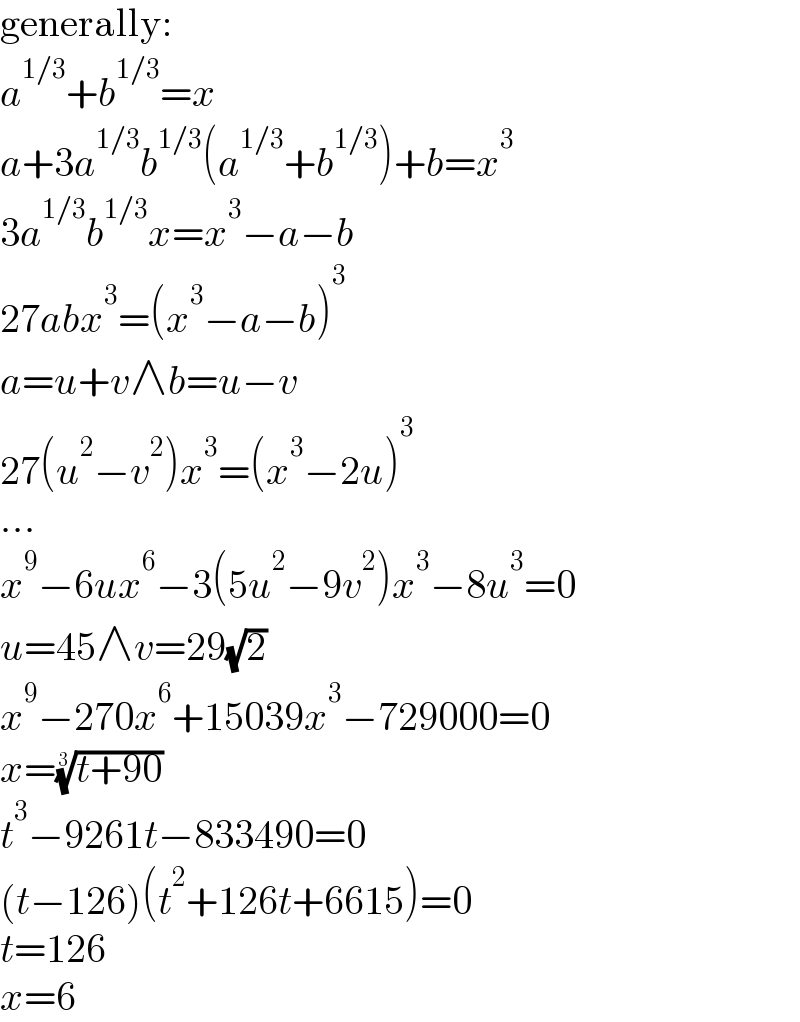
generally: a^(1/3) +b^(1/3) =x a+3a^(1/3) b^(1/3) (a^(1/3) +b^(1/3) )+b=x^3 3a^(1/3) b^(1/3) x=x^3 −a−b 27abx^3 =(x^3 −a−b)^3 a=u+v∧b=u−v 27(u^2 −v^2 )x^3 =(x^3 −2u)^3 ... x^9 −6ux^6 −3(5u^2 −9v^2 )x^3 −8u^3 =0 u=45∧v=29(√2) x^9 −270x^6 +15039x^3 −729000=0 x=((t+90))^(1/3) t^3 −9261t−833490=0 (t−126)(t^2 +126t+6615)=0 t=126 x=6

$$\mathrm{generally}: \\ $$$${a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} ={x} \\ $$$${a}+\mathrm{3}{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} \left({a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} \right)+{b}={x}^{\mathrm{3}} \\ $$$$\mathrm{3}{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} {x}={x}^{\mathrm{3}} −{a}−{b} \\ $$$$\mathrm{27}{abx}^{\mathrm{3}} =\left({x}^{\mathrm{3}} −{a}−{b}\right)^{\mathrm{3}} \\ $$$${a}={u}+{v}\wedge{b}={u}−{v} \\ $$$$\mathrm{27}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right){x}^{\mathrm{3}} =\left({x}^{\mathrm{3}} −\mathrm{2}{u}\right)^{\mathrm{3}} \\ $$$$... \\ $$$${x}^{\mathrm{9}} −\mathrm{6}{ux}^{\mathrm{6}} −\mathrm{3}\left(\mathrm{5}{u}^{\mathrm{2}} −\mathrm{9}{v}^{\mathrm{2}} \right){x}^{\mathrm{3}} −\mathrm{8}{u}^{\mathrm{3}} =\mathrm{0} \\ $$$${u}=\mathrm{45}\wedge{v}=\mathrm{29}\sqrt{\mathrm{2}} \\ $$$${x}^{\mathrm{9}} −\mathrm{270}{x}^{\mathrm{6}} +\mathrm{15039}{x}^{\mathrm{3}} −\mathrm{729000}=\mathrm{0} \\ $$$${x}=\sqrt[{\mathrm{3}}]{{t}+\mathrm{90}} \\ $$$${t}^{\mathrm{3}} −\mathrm{9261}{t}−\mathrm{833490}=\mathrm{0} \\ $$$$\left({t}−\mathrm{126}\right)\left({t}^{\mathrm{2}} +\mathrm{126}{t}+\mathrm{6615}\right)=\mathrm{0} \\ $$$${t}=\mathrm{126} \\ $$$${x}=\mathrm{6} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com