
Question Number 43621 by ajfour last updated on 12/Sep/18
Commented by math1967 last updated on 13/Sep/18
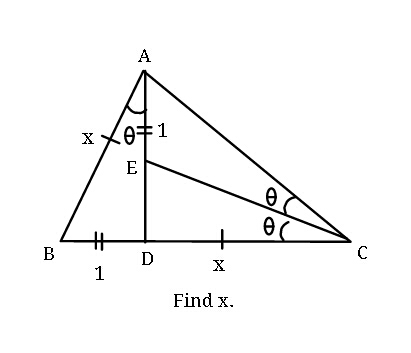
![AD=(√(x^2 −1)) ,AC=(√(x^2 +x^2 −1))=(√(2x^2 −1)) △ABD∼△CED ∴((ED)/x)=(1/(√(x^2 −1))) ⇒ED=(x/(√(x^2 −1))) Again ((AC)/(CD))=((AE)/(ED)) [CE is bisector] ⇒((√(2x^2 −1))/x)=((√(x^2 −1))/x) now I cannot find x Is it any mistake?](Q43646.png)
$${AD}=\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\:\:,{AC}=\sqrt{{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{1}}=\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\bigtriangleup{ABD}\sim\bigtriangleup{CED}\:\therefore\frac{{ED}}{{x}}=\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\Rightarrow{ED}=\frac{{x}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${Again}\:\frac{{AC}}{{CD}}=\frac{{AE}}{{ED}}\:\:\:\:\left[{CE}\:{is}\:{bisector}\right] \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}}{{x}}=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}} \\ $$$${now}\:{I}\:{cannot}\:{find}\:{x}\: \\ $$$${Is}\:{it}\:{any}\:{mistake}? \\ $$
Commented by MJS last updated on 13/Sep/18
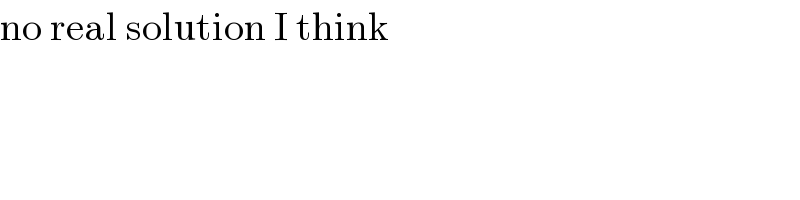
$$\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{I}\:\mathrm{think} \\ $$
Answered by ajfour last updated on 13/Sep/18
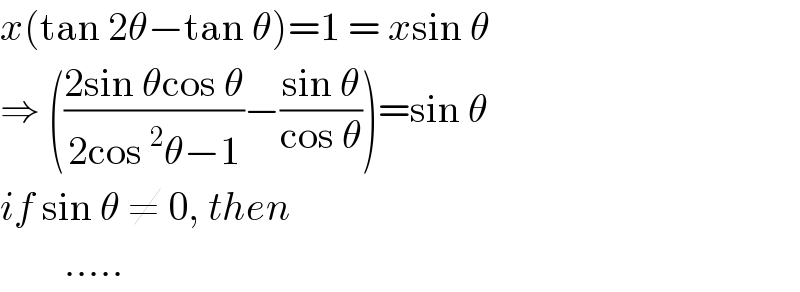
$${x}\left(\mathrm{tan}\:\mathrm{2}\theta−\mathrm{tan}\:\theta\right)=\mathrm{1}\:=\:{x}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\left(\frac{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}}−\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right)=\mathrm{sin}\:\theta \\ $$$${if}\:\mathrm{sin}\:\theta\:\neq\:\mathrm{0},\:{then} \\ $$$$\:\:\:\:\:\:\:\:.....\:\: \\ $$
