
Question Number 43147 by rahul 19 last updated on 07/Sep/18
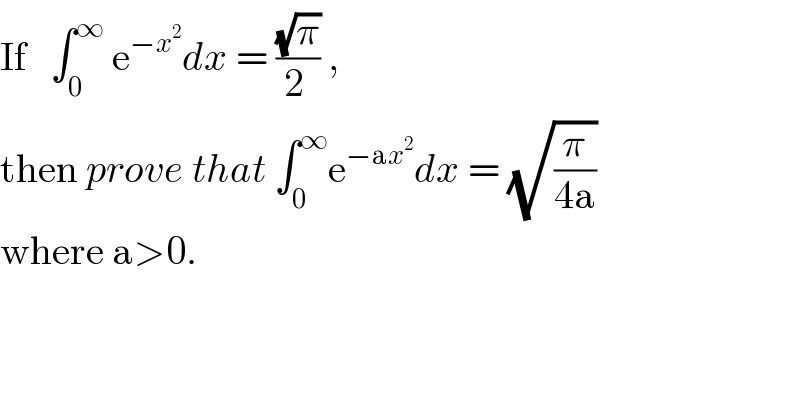
$$\mathrm{If}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}\:=\:\frac{\sqrt{\pi}}{\mathrm{2}\:}\:, \\ $$ $$\mathrm{then}\:{prove}\:{that}\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{a}{x}^{\mathrm{2}} } {dx}\:=\:\sqrt{\frac{\pi}{\mathrm{4a}}} \\ $$ $$\mathrm{where}\:\mathrm{a}>\mathrm{0}. \\ $$
Commented byMrW3 last updated on 07/Sep/18
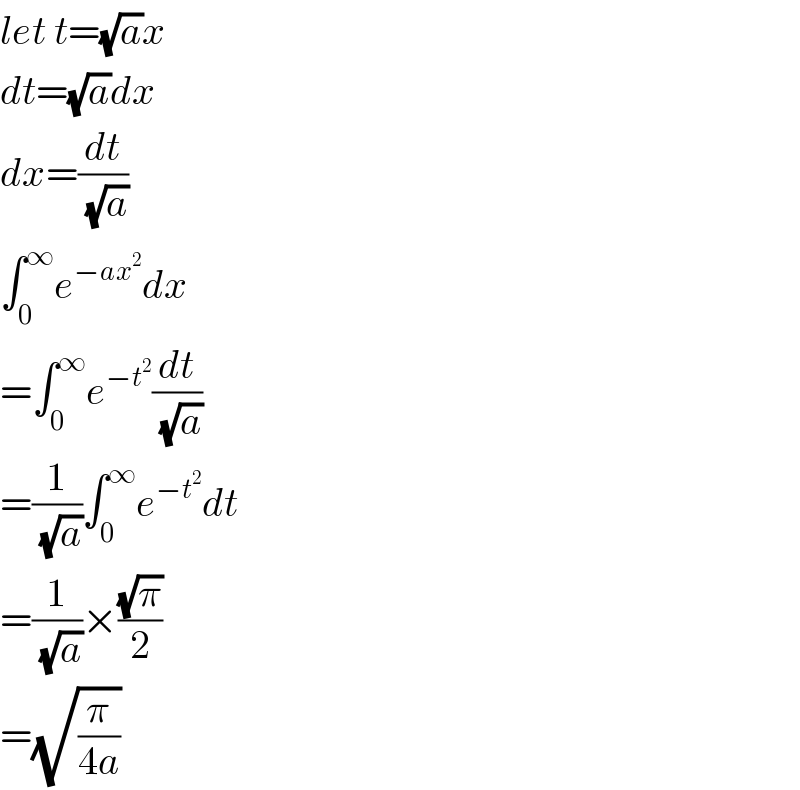
$${let}\:{t}=\sqrt{{a}}{x} \\ $$ $${dt}=\sqrt{{a}}{dx} \\ $$ $${dx}=\frac{{dt}}{\sqrt{{a}}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}^{\mathrm{2}} } {dx} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } \frac{{dt}}{\sqrt{{a}}} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{{a}}}×\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$ $$=\sqrt{\frac{\pi}{\mathrm{4}{a}}} \\ $$
Commented byrahul 19 last updated on 07/Sep/18
thank you sir ��
