
Question Number 42316 by Raj Singh last updated on 23/Aug/18

Commented by Raj Singh last updated on 23/Aug/18

$${how}\:{x}=\mathrm{4}\:{y}=\mathrm{9} \\ $$
Commented by maxmathsup by imad last updated on 23/Aug/18
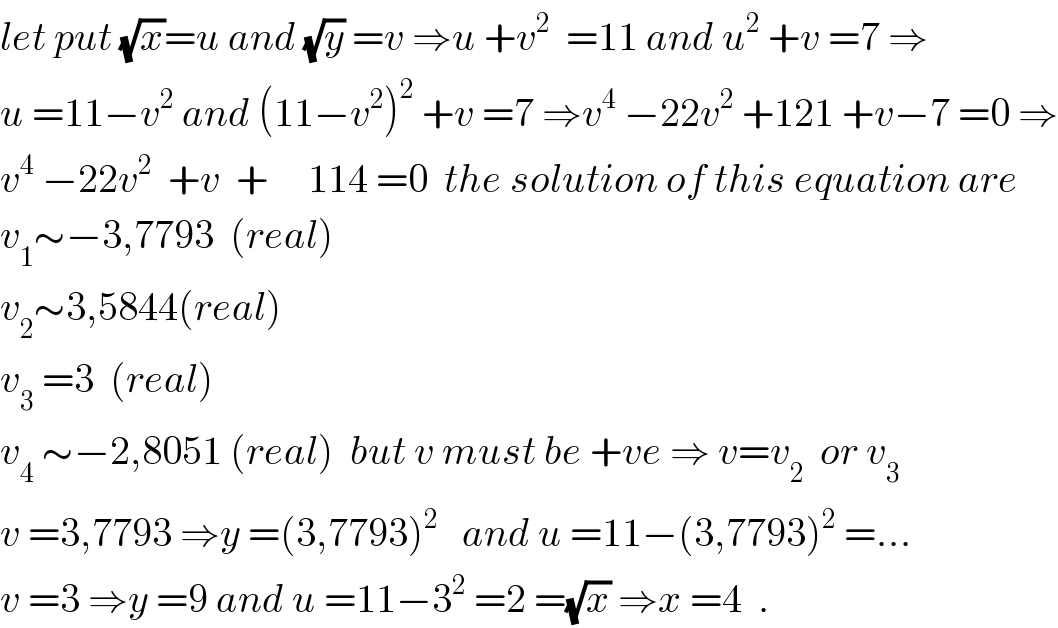
$${let}\:{put}\:\sqrt{{x}}={u}\:{and}\:\sqrt{{y}}\:={v}\:\Rightarrow{u}\:+{v}^{\mathrm{2}} \:\:=\mathrm{11}\:{and}\:{u}^{\mathrm{2}} \:+{v}\:=\mathrm{7}\:\Rightarrow \\ $$$${u}\:=\mathrm{11}−{v}^{\mathrm{2}} \:{and}\:\left(\mathrm{11}−{v}^{\mathrm{2}} \right)^{\mathrm{2}} \:+{v}\:=\mathrm{7}\:\Rightarrow{v}^{\mathrm{4}} \:−\mathrm{22}{v}^{\mathrm{2}} \:+\mathrm{121}\:+{v}−\mathrm{7}\:=\mathrm{0}\:\Rightarrow \\ $$$${v}^{\mathrm{4}} \:−\mathrm{22}{v}^{\mathrm{2}} \:\:+{v}\:\:+\:\:\:\:\:\mathrm{114}\:=\mathrm{0}\:\:{the}\:{solution}\:{of}\:{this}\:{equation}\:{are} \\ $$$${v}_{\mathrm{1}} \sim−\mathrm{3},\mathrm{7793}\:\:\left({real}\right) \\ $$$${v}_{\mathrm{2}} \sim\mathrm{3},\mathrm{5844}\left({real}\right) \\ $$$${v}_{\mathrm{3}} \:=\mathrm{3}\:\:\left({real}\right) \\ $$$${v}_{\mathrm{4}} \:\sim−\mathrm{2},\mathrm{8051}\:\left({real}\right)\:\:{but}\:{v}\:{must}\:{be}\:+{ve}\:\Rightarrow\:{v}={v}_{\mathrm{2}} \:\:{or}\:{v}_{\mathrm{3}} \\ $$$${v}\:=\mathrm{3},\mathrm{7793}\:\Rightarrow{y}\:=\left(\mathrm{3},\mathrm{7793}\right)^{\mathrm{2}} \:\:\:{and}\:{u}\:=\mathrm{11}−\left(\mathrm{3},\mathrm{7793}\right)^{\mathrm{2}} \:=... \\ $$$${v}\:=\mathrm{3}\:\Rightarrow{y}\:=\mathrm{9}\:{and}\:{u}\:=\mathrm{11}−\mathrm{3}^{\mathrm{2}} \:=\mathrm{2}\:=\sqrt{{x}}\:\Rightarrow{x}\:=\mathrm{4}\:\:. \\ $$
Answered by behi83417@gmail.com last updated on 23/Aug/18
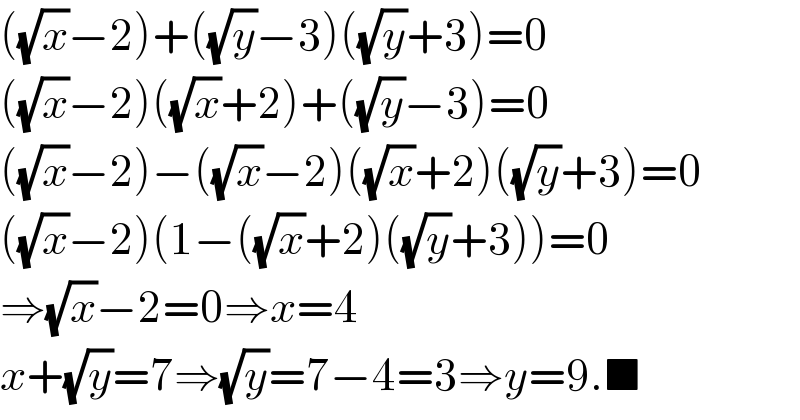
$$\left(\sqrt{{x}}−\mathrm{2}\right)+\left(\sqrt{{y}}−\mathrm{3}\right)\left(\sqrt{{y}}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\sqrt{{x}}−\mathrm{2}\right)\left(\sqrt{{x}}+\mathrm{2}\right)+\left(\sqrt{{y}}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\sqrt{{x}}−\mathrm{2}\right)−\left(\sqrt{{x}}−\mathrm{2}\right)\left(\sqrt{{x}}+\mathrm{2}\right)\left(\sqrt{{y}}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\sqrt{{x}}−\mathrm{2}\right)\left(\mathrm{1}−\left(\sqrt{{x}}+\mathrm{2}\right)\left(\sqrt{{y}}+\mathrm{3}\right)\right)=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}−\mathrm{2}=\mathrm{0}\Rightarrow{x}=\mathrm{4} \\ $$$${x}+\sqrt{{y}}=\mathrm{7}\Rightarrow\sqrt{{y}}=\mathrm{7}−\mathrm{4}=\mathrm{3}\Rightarrow{y}=\mathrm{9}.\blacksquare \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Aug/18
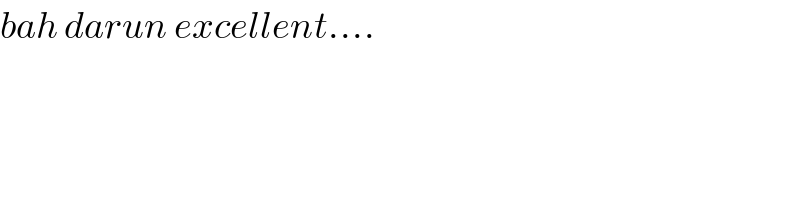
$${bah}\:{darun}\:{excellent}.... \\ $$
Commented by Joel578 last updated on 23/Aug/18
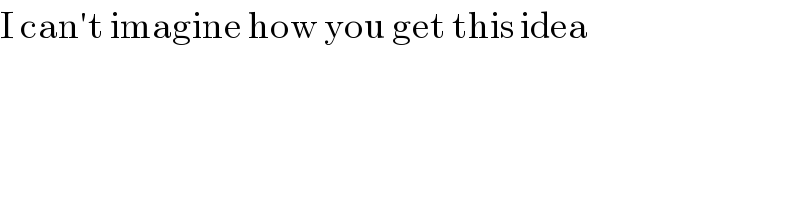
$$\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{imagine}\:\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{this}\:\mathrm{idea} \\ $$
Commented by maxmathsup by imad last updated on 23/Aug/18
$${i}\:{think}\:{sir}\:{behi}\:{have}\:{played}\:{a}\:{match}\:{criket}\:\:{with}\:{this}\:{equation}... \\ $$
