
Question Number 42195 by math khazana by abdo last updated on 20/Aug/18
![let p(x)=x^(10) −1 1) find roots of p(x) 2) factorize i nside C[x] p(x{ 3) factorize inside R[x] p(x) .](Q42195.png)
$${let}\:{p}\left({x}\right)={x}^{\mathrm{10}} −\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{roots}\:{of}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{factorize}\:{i}\:{nside}\:\:{C}\left[{x}\right]\:{p}\left({x}\left\{\right.\right. \\ $$$$\left.\mathrm{3}\right)\:{factorize}\:{inside}\:{R}\left[{x}\right]\:{p}\left({x}\right)\:. \\ $$
Answered by maxmathsup by imad last updated on 21/Aug/18
![1) p(z)=0 ⇔ z^(10) −1=0 ⇔ z^(10) =1 if z=r e^(iθ) we get r^(10) e^(i10θ) =e^(i2kπ) ⇒ r =1 and θ =((2kπ)/(10)) =((kπ)/5) so the roots of p(x)are z_k =e^(i((kπ)/5)) with k∈[[0,9]] 2) p(x) =Π_(k=0) ^9 (x−z_k ) =Π_(k=0) ^9 (x−e^((ikπ)/5) ) 3) generally let decmpose q(x) =x^(2n) −1 the roots are z_k =e^((ikn)/n) with k ∈[[0,2n−1]] ⇒q(x)=Π_(k=0) ^(2n−1) (x−e^((ikπ)/n) ) but z_0 =1 z_1 =e^((iπ)/n) z_2 =e^((i2π)/n) z_(n−1) =e^((i(n−1)π)/n) z_n =−1 z_(n+1) =e^((i(n+1)π)/n) ...z_(2n−1) =e^((i(2n−1)π)/n) ⇒z_1 ^− =e^(−((iπ)/n)) =e^(2iπ−((iπ)/n)) = e^(i(((2n−1)π)/n)) =z_(2n−1) ^− .....⇒z_(2n−p) =z_p ^− ⇒ q(x) =(x^2 −1) Π_(k=1) ^(n−1) (x−z_k )(x−z_k ^− )=(x^2 −1)Π_(k=1) ^(n−1) (x^2 −2cos(((kπ)/n))x +1) for n=5 we get p(x)=(x^2 −1)Π_(k=1) ^4 (x^2 −2cos(((kπ)/5))x +1) =(x^2 −1)(x^2 −2cos((π/5))x +1)(x^2 −2cos(((2π)/5))x+1)(x^2 −2cos(((3π)/5))x+1)(x^2 −2cos(((4π)/5))x+1). =(x^2 −2cos((π/5))x+1)(x^2 +2cos((π/5))x+1)(x^2 −2cos(((2π)/5))x+1)(x^2 +2cos(((2π)/5))x+1).](Q42283.png)
$$\left.\mathrm{1}\right)\:{p}\left({z}\right)=\mathrm{0}\:\Leftrightarrow\:{z}^{\mathrm{10}} −\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{z}^{\mathrm{10}} \:=\mathrm{1}\:\:{if}\:{z}={r}\:{e}^{{i}\theta} \:\:{we}\:{get}\:{r}^{\mathrm{10}} {e}^{{i}\mathrm{10}\theta} \:={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow \\ $$$${r}\:=\mathrm{1}\:{and}\:\theta\:=\frac{\mathrm{2}{k}\pi}{\mathrm{10}}\:=\frac{{k}\pi}{\mathrm{5}}\:\:{so}\:{the}\:{roots}\:{of}\:{p}\left({x}\right){are}\:{z}_{{k}} ={e}^{{i}\frac{{k}\pi}{\mathrm{5}}} \:\:{with}\:{k}\in\left[\left[\mathrm{0},\mathrm{9}\right]\right] \\ $$$$\left.\mathrm{2}\right)\:{p}\left({x}\right)\:=\prod_{{k}=\mathrm{0}} ^{\mathrm{9}} \left({x}−{z}_{{k}} \right)\:=\prod_{{k}=\mathrm{0}} ^{\mathrm{9}} \left({x}−{e}^{\frac{{ik}\pi}{\mathrm{5}}} \right) \\ $$$$\left.\mathrm{3}\right)\:{generally}\:{let}\:{decmpose}\:{q}\left({x}\right)\:={x}^{\mathrm{2}{n}} \:−\mathrm{1}\:{the}\:{roots}\:{are}\:{z}_{{k}} ={e}^{\frac{{ikn}}{{n}}} \:{with} \\ $$$${k}\:\in\left[\left[\mathrm{0},\mathrm{2}{n}−\mathrm{1}\right]\right]\:\Rightarrow{q}\left({x}\right)=\prod_{{k}=\mathrm{0}} ^{\mathrm{2}{n}−\mathrm{1}} \left({x}−{e}^{\frac{{ik}\pi}{{n}}} \right)\:\:{but}\:{z}_{\mathrm{0}} =\mathrm{1}\:\:{z}_{\mathrm{1}} ={e}^{\frac{{i}\pi}{{n}}} \\ $$$${z}_{\mathrm{2}} ={e}^{\frac{{i}\mathrm{2}\pi}{{n}}} \:\:\:\:\:\:\:{z}_{{n}−\mathrm{1}} ={e}^{\frac{{i}\left({n}−\mathrm{1}\right)\pi}{{n}}} \:\:{z}_{{n}} =−\mathrm{1}\:\:\:\:{z}_{{n}+\mathrm{1}} ={e}^{\frac{{i}\left({n}+\mathrm{1}\right)\pi}{{n}}} \:\:\:...{z}_{\mathrm{2}{n}−\mathrm{1}} ={e}^{\frac{{i}\left(\mathrm{2}{n}−\mathrm{1}\right)\pi}{{n}}} \\ $$$$\Rightarrow\overset{−} {{z}}_{\mathrm{1}} \:\:={e}^{−\frac{{i}\pi}{{n}}} \:={e}^{\mathrm{2}{i}\pi−\frac{{i}\pi}{{n}}} \:=\:{e}^{{i}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\pi}{{n}}} \:\:=\overset{−} {{z}}_{\mathrm{2}{n}−\mathrm{1}} \:\:.....\Rightarrow{z}_{\mathrm{2}{n}−{p}} \:=\overset{−} {{z}}_{{p}} \:\Rightarrow \\ $$$${q}\left({x}\right)\:=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left({x}−{z}_{{k}} \right)\left({x}−\overset{−} {{z}}_{{k}} \right)=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{{k}\pi}{{n}}\right){x}\:+\mathrm{1}\right) \\ $$$${for}\:{n}=\mathrm{5}\:\:{we}\:{get}\:\:{p}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\prod_{{k}=\mathrm{1}} ^{\mathrm{4}} \left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{{k}\pi}{\mathrm{5}}\right){x}\:+\mathrm{1}\right) \\ $$$$=\left({x}^{\mathrm{2}} \:−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{5}}\right){x}\:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right). \\ $$$$=\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right). \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 21/Aug/18
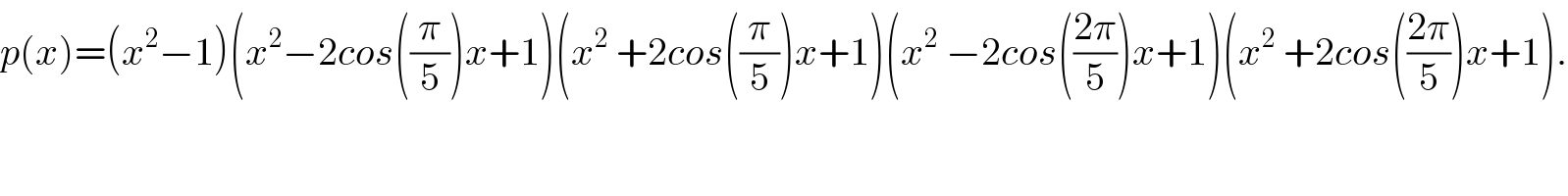
$${p}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right){x}+\mathrm{1}\right). \\ $$
