
Question Number 41049 by prof Abdo imad last updated on 01/Aug/18
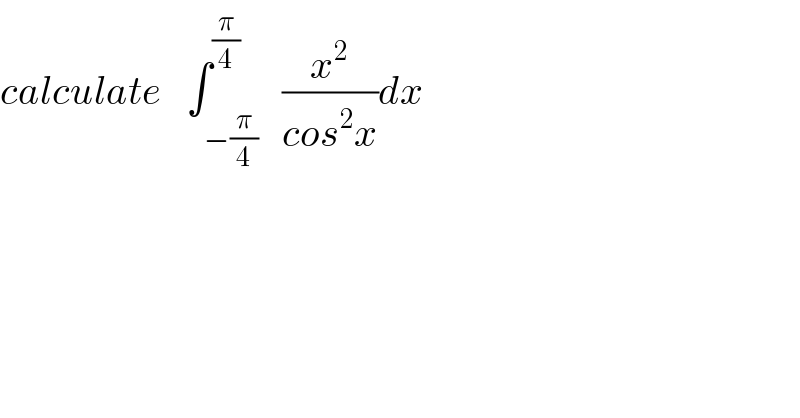
$${calculate}\:\:\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{x}^{\mathrm{2}} }{{cos}^{\mathrm{2}} {x}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 02/Aug/18
![let I = ∫_(−(π/4)) ^(π/4) (x^2 /(cos^2 x))dx ⇒ I =∫_(−(π/4)) ^(π/4) (1+tan^2 x)x^2 dx changement tanx =t give I = ∫_(−1) ^1 (1+t^2 )(arctant)^2 (dt/(1+t^2 )) = 2∫_0 ^1 (arctant)^2 dt by parts I = 2{ [t (arctant)^2 ]_0 ^1 −∫_0 ^1 t ((2arctan(t))/(1+t^2 ))dt} =2{(π^2 /(16)) − ∫_0 ^1 ((2t arctan(t))/(1+t^2 ))} =(π^2 /8) −4 ∫_0 ^1 ((t arctan(t))/(1+t^2 )) dt let ϕ(x) =∫_0 ^1 ((t arctan(xt))/(1+t^2 )) dt ⇒ϕ^′ (x) = ∫_0 ^1 (t^2 /((1+x^2 t^2 )(1+t^2 )))dt ϕ^′ (x) =_(xt =u) ∫_0 ^x (u^2 /(x^2 (1+u^2 )(1+(u^2 /x^2 )))) (du/x) = ∫_0 ^x (u^2 /(x(1+u^2 )(x^2 +u^2 )))du =(1/x) ∫_0 ^1 (u^2 /((u^2 +1)( u^2 +x^2 )))du let decompose F(u) = (u^2 /((u^2 +1)(u^2 +x^2 ))) ⇒F(u) = ((au+b)/(u^2 +1)) +((cu +d)/(u^2 +x^2 )) F(−u) =F(u) ⇒((−au +b)/(u^2 +1)) +((−cu +d)/(u^2 +x^2 )) =F(u) ⇒a=c=0 ⇒ F(u) = (b/(u^2 +1)) +(d/(u^2 +x^2 )) lim_(u→+∞) u^2 F(u) =1 =b+d ⇒d=1−b ⇒ F(u) =(b/(u^2 +1)) +((1−b)/(u^2 +x^2 )) ⇒F(0) =0 =b +((1−b)/x^2 ) =(1/x^2 ) +(1−(1/x^2 ))b ⇒ −(1/x^2 ) =(((x^2 −1)b)/x^2 ) ⇒b =(1/(1−x^2 )) ⇒F(u) =(1/((1−x^2 )(u^2 +1))) +((1−(1/(1−x^2 )))/(u^2 +x^2 )) = (1/((1−x^2 )(u^2 +1))) −(x^2 /((1−x^2 )(u^2 +x^2 ))) ⇒F(u) =(1/(1−x^2 )){(1/(u^2 +1)) −(x^2 /(u^2 +x^2 ))} ϕ^′ (x) =(1/x)∫_0 ^x F(u)du =(1/(x(1−x^2 ))){ ∫_0 ^x (du/(1+u^2 )) −x^2 ∫_0 ^x (du/(u^2 +x^2 ))} =((arctanx)/(x(1−x^2 ))) −(x/(1−x^2 )) ∫_0 ^x (du/(u^2 +x^2 )) but ∫_0 ^x (du/(u^2 +x^2 )) du =_(u=xt) ∫_0 ^1 ((xdt)/(x^2 t^2 +x^2 )) =(1/x) ∫_0 ^1 (dt/(t^2 +1)) =(π/(4x)) ⇒ ϕ^′ (x) = ((arctan(x))/(x(1−x^2 ))) −(π/(4(1−x^2 ))) ( for x^2 ≠1) ⇒](Q41126.png)
$${let}\:\:{I}\:\:\:=\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{x}^{\mathrm{2}} }{{cos}^{\mathrm{2}} {x}}{dx}\:\Rightarrow\:{I}\:\:=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){x}^{\mathrm{2}} {dx}\:{changement}\:{tanx}\:={t} \\ $$$${give}\:{I}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({arctant}\right)^{\mathrm{2}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({arctant}\right)^{\mathrm{2}} {dt}\:{by}\:{parts} \\ $$$${I}\:=\:\mathrm{2}\left\{\:\left[{t}\:\left({arctant}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}\:\frac{\mathrm{2}{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\right\} \\ $$$$=\mathrm{2}\left\{\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{t}\:{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\right\}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}\:{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${let}\:\varphi\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}\:{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:\Rightarrow\varphi^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}\: \\ $$$$\varphi^{'} \left({x}\right)\:\:=_{{xt}\:={u}} \:\:\:\:\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\:\:\:\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:\frac{{du}}{{x}} \\ $$$$=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\:\:\frac{{u}^{\mathrm{2}} }{{x}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+{u}^{\mathrm{2}} \right)}{du}\:=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\:{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\:\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}\:\Rightarrow{F}\left({u}\right)\:=\:\frac{{au}+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} } \\ $$$${F}\left(−{u}\right)\:={F}\left({u}\right)\:\Rightarrow\frac{−{au}\:+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{cu}\:+{d}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:={F}\left({u}\right)\:\Rightarrow{a}={c}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\:\frac{{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{d}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {u}^{\mathrm{2}} {F}\left({u}\right)\:=\mathrm{1}\:={b}+{d}\:\Rightarrow{d}=\mathrm{1}−{b}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{{b}}{{u}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\mathrm{1}−{b}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:\Rightarrow{F}\left(\mathrm{0}\right)\:=\mathrm{0}\:={b}\:+\frac{\mathrm{1}−{b}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){b}\:\Rightarrow \\ $$$$\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){b}}{{x}^{\mathrm{2}} }\:\Rightarrow{b}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:−\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\left\{\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{{x}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\right\} \\ $$$$\varphi^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{{x}} \:{F}\left({u}\right){du}\:=\frac{\mathrm{1}}{{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\left\{\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:−{x}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{{arctanx}}{{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:−\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{du}}{{u}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{but} \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:{du}\:=_{{u}={xt}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{xdt}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\mathrm{4}{x}}\:\Rightarrow \\ $$$$\varphi^{'} \left({x}\right)\:=\:\frac{{arctan}\left({x}\right)}{{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:−\frac{\pi}{\mathrm{4}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:\left(\:{for}\:{x}^{\mathrm{2}} \:\neq\mathrm{1}\right)\:\Rightarrow \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 02/Aug/18
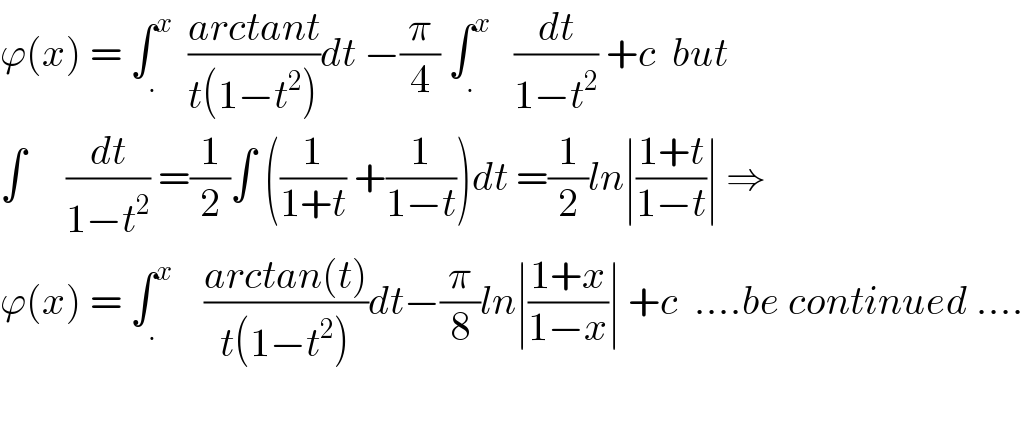
$$\varphi\left({x}\right)\:=\:\int_{.} ^{{x}} \:\:\frac{{arctant}}{{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt}\:−\frac{\pi}{\mathrm{4}}\:\int_{.} ^{{x}} \:\:\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+{c}\:\:{but} \\ $$$$\int\:\:\:\:\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{\mathrm{1}+{t}}\:+\frac{\mathrm{1}}{\mathrm{1}−{t}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\:\Rightarrow \\ $$$$\varphi\left({x}\right)\:=\:\int_{.} ^{{x}} \:\:\:\:\frac{{arctan}\left({t}\right)}{{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt}−\frac{\pi}{\mathrm{8}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:+{c}\:\:....{be}\:{continued}\:.... \\ $$$$ \\ $$
