
Previous in Relation and Functions Next in Relation and Functions
Question Number 40878 by prof Abdo imad last updated on 28/Jul/18
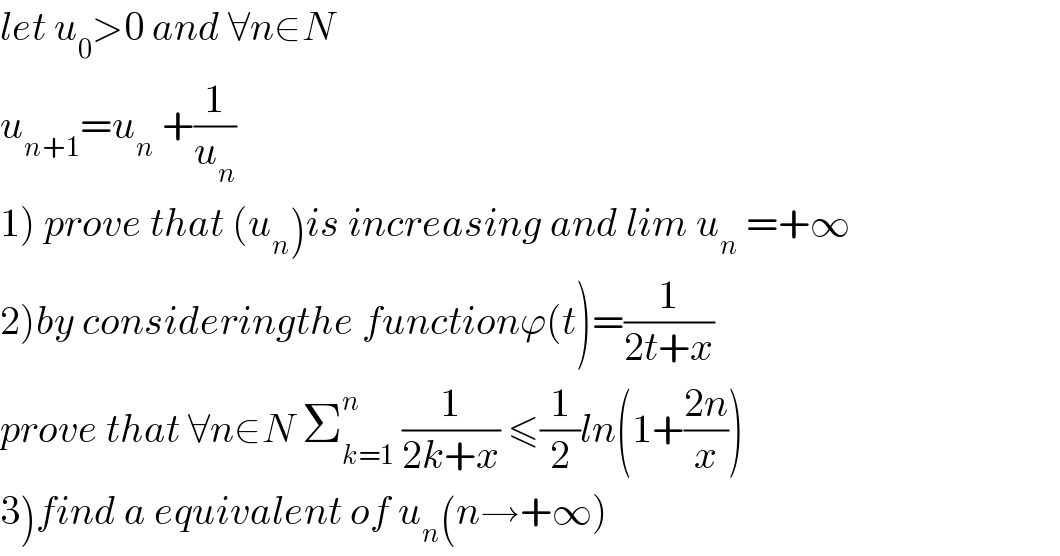
$${let}\:{u}_{\mathrm{0}} >\mathrm{0}\:{and}\:\forall{n}\in{N} \\ $$ $${u}_{{n}+\mathrm{1}} ={u}_{{n}} \:+\frac{\mathrm{1}}{{u}_{{n}} } \\ $$ $$\left.\mathrm{1}\right)\:{prove}\:{that}\:\left({u}_{{n}} \right){is}\:{increasing}\:{and}\:{lim}\:{u}_{{n}} \:=+\infty \\ $$ $$\left.\mathrm{2}\right){by}\:{consideringthe}\:{function}\varphi\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}{t}+{x}} \\ $$ $${prove}\:{that}\:\forall{n}\in{N}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+{x}}\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{\mathrm{2}{n}}{{x}}\right) \\ $$ $$\left.\mathrm{3}\right){find}\:{a}\:{equivalent}\:{of}\:{u}_{{n}} \left({n}\rightarrow+\infty\right) \\ $$
