
Question Number 40640 by upadhyayrakhi20@gmail.com last updated on 25/Jul/18

$${evaluate} \\ $$$$\mathrm{sin}\:\mathrm{72}\:^{.} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18
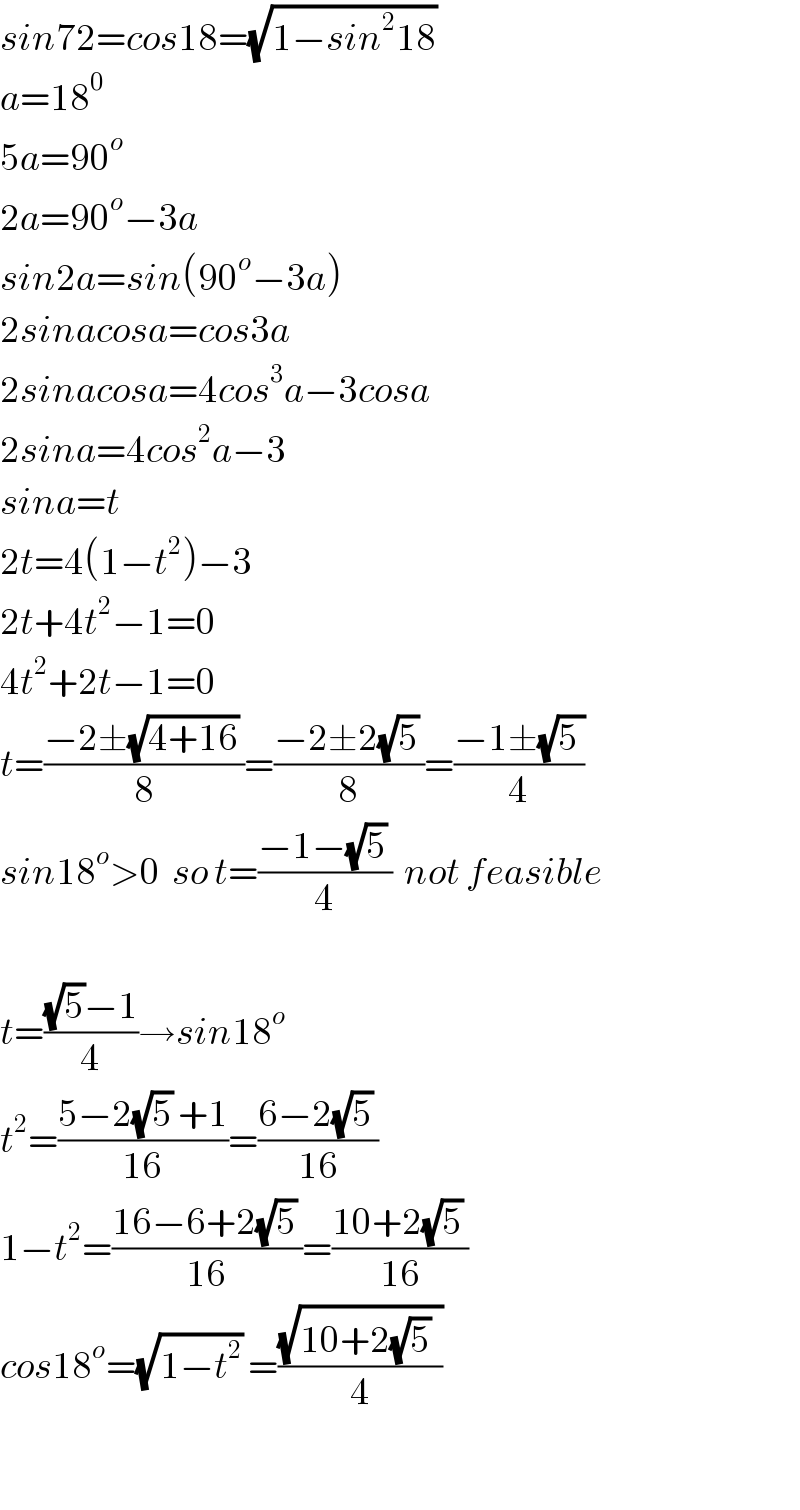
$${sin}\mathrm{72}={cos}\mathrm{18}=\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \mathrm{18}}\: \\ $$$${a}=\mathrm{18}^{\mathrm{0}} \\ $$$$\mathrm{5}{a}=\mathrm{90}^{{o}} \\ $$$$\mathrm{2}{a}=\mathrm{90}^{{o}} −\mathrm{3}{a} \\ $$$${sin}\mathrm{2}{a}={sin}\left(\mathrm{90}^{{o}} −\mathrm{3}{a}\right) \\ $$$$\mathrm{2}{sinacosa}={cos}\mathrm{3}{a} \\ $$$$\mathrm{2}{sinacosa}=\mathrm{4}{cos}^{\mathrm{3}} {a}−\mathrm{3}{cosa} \\ $$$$\mathrm{2}{sina}=\mathrm{4}{cos}^{\mathrm{2}} {a}−\mathrm{3} \\ $$$${sina}={t} \\ $$$$\mathrm{2}{t}=\mathrm{4}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−\mathrm{3} \\ $$$$\mathrm{2}{t}+\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{16}}\:}{\mathrm{8}}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{5}}\:}{\mathrm{8}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}\:}}{\mathrm{4}} \\ $$$${sin}\mathrm{18}^{{o}} >\mathrm{0}\:\:{so}\:{t}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}\:}{\mathrm{4}}\:\:{not}\:{feasible} \\ $$$$ \\ $$$${t}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\rightarrow{sin}\mathrm{18}^{{o}} \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\:+\mathrm{1}}{\mathrm{16}}=\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\:}{\mathrm{16}} \\ $$$$\mathrm{1}−{t}^{\mathrm{2}} =\frac{\mathrm{16}−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\:}{\mathrm{16}}=\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\:}{\mathrm{16}} \\ $$$${cos}\mathrm{18}^{{o}} =\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\:\:}}{\mathrm{4}} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 25/Jul/18

$$\mathrm{great}\:.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18

$${thank}\:{you}\:{sir}... \\ $$
Commented by upadhyayrakhi20@gmail.com last updated on 25/Jul/18

$$\mathrm{thnx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18

$${its}\:{ok}... \\ $$
Answered by MJS last updated on 25/Jul/18
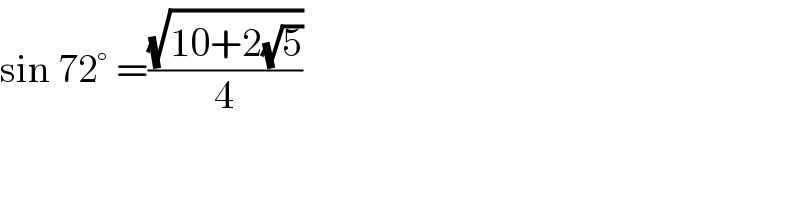
$$\mathrm{sin}\:\mathrm{72}°\:=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$
