
Question Number 40519 by rahul 19 last updated on 23/Jul/18

Commented by rahul 19 last updated on 23/Jul/18
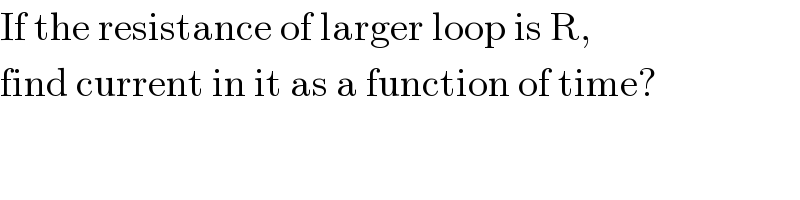
$$\mathrm{If}\:\mathrm{the}\:\mathrm{resistance}\:\mathrm{of}\:\mathrm{larger}\:\mathrm{loop}\:\mathrm{is}\:\mathrm{R}, \\ $$$$\mathrm{find}\:\mathrm{current}\:\mathrm{in}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{time}? \\ $$
Answered by ajfour last updated on 23/Jul/18
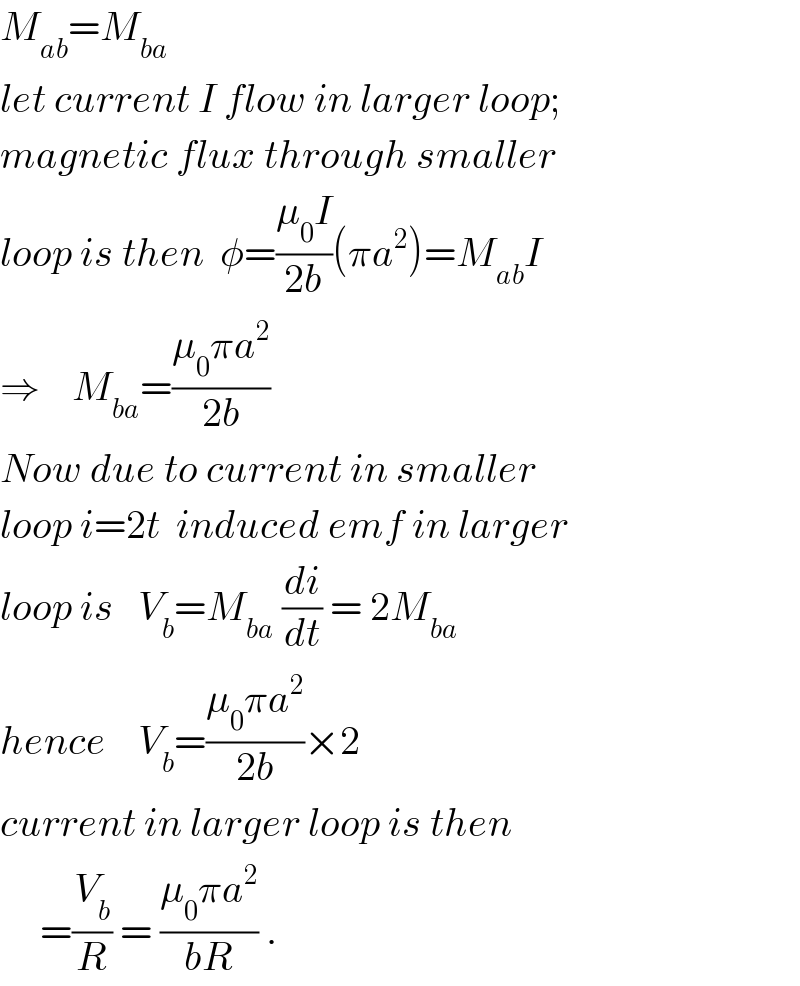
$${M}_{{ab}} ={M}_{{ba}} \\ $$$${let}\:{current}\:{I}\:{flow}\:{in}\:{larger}\:{loop}; \\ $$$${magnetic}\:{flux}\:{through}\:{smaller} \\ $$$${loop}\:{is}\:{then}\:\:\phi=\frac{\mu_{\mathrm{0}} {I}}{\mathrm{2}{b}}\left(\pi{a}^{\mathrm{2}} \right)={M}_{{ab}} {I} \\ $$$$\Rightarrow\:\:\:\:{M}_{{ba}} =\frac{\mu_{\mathrm{0}} \pi{a}^{\mathrm{2}} }{\mathrm{2}{b}} \\ $$$${Now}\:{due}\:{to}\:{current}\:{in}\:{smaller} \\ $$$${loop}\:{i}=\mathrm{2}{t}\:\:{induced}\:{emf}\:{in}\:{larger} \\ $$$${loop}\:{is}\:\:\:{V}_{{b}} ={M}_{{ba}} \:\frac{{di}}{{dt}}\:=\:\mathrm{2}{M}_{{ba}} \\ $$$${hence}\:\:\:\:{V}_{{b}} =\frac{\mu_{\mathrm{0}} \pi{a}^{\mathrm{2}} }{\mathrm{2}{b}}×\mathrm{2} \\ $$$${current}\:{in}\:{larger}\:{loop}\:{is}\:{then} \\ $$$$\:\:\:\:\:=\frac{{V}_{{b}} }{{R}}\:=\:\frac{\mu_{\mathrm{0}} \pi{a}^{\mathrm{2}} }{{bR}}\:. \\ $$
Commented by rahul 19 last updated on 23/Jul/18
thank you both sirs ������
Commented by rahul 19 last updated on 23/Jul/18

$$\mathrm{This}\:\mathrm{result}\:\mathrm{shows}\:\mathrm{current}\:\mathrm{independent} \\ $$$$\mathrm{of}\:\mathrm{time}\:\mathrm{in}\:\mathrm{larger}\:\mathrm{loop}.\:\mathrm{But}\:\mathrm{if}\:\mathrm{we}\:\mathrm{take}\:\mathrm{some}\:\mathrm{instant} \\ $$$$\mathrm{say}\:\mathrm{t}=\mathrm{0}\:,\:\mathrm{then}\:{why}\:\:\mathrm{will}\:\mathrm{current}\:\mathrm{flow}\:? \\ $$$$?\mathrm{And}\:\mathrm{what}\:\mathrm{about}\:\mathrm{t}=\infty\:?..... \\ $$
Commented by ajfour last updated on 23/Jul/18
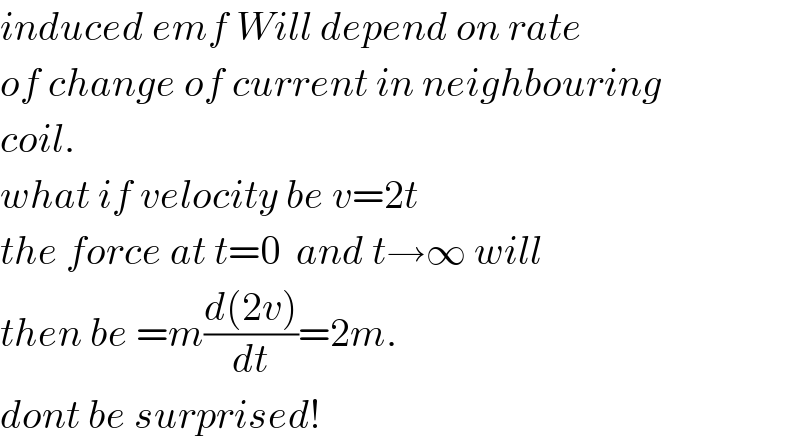
$${induced}\:{emf}\:{Will}\:{depend}\:{on}\:{rate} \\ $$$${of}\:{change}\:{of}\:{current}\:{in}\:{neighbouring} \\ $$$${coil}. \\ $$$${what}\:{if}\:{velocity}\:{be}\:{v}=\mathrm{2}{t} \\ $$$${the}\:{force}\:{at}\:{t}=\mathrm{0}\:\:{and}\:{t}\rightarrow\infty\:{will} \\ $$$${then}\:{be}\:={m}\frac{{d}\left(\mathrm{2}{v}\right)}{{dt}}=\mathrm{2}{m}. \\ $$$${dont}\:{be}\:{surprised}! \\ $$
Commented by rahul 19 last updated on 23/Jul/18
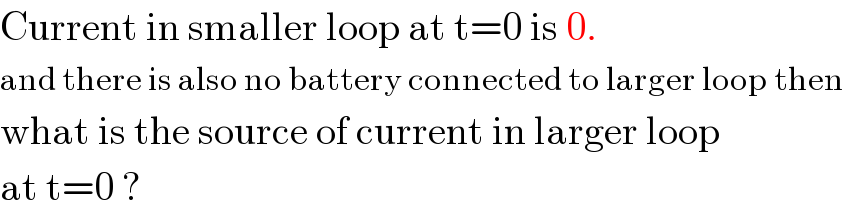
$$\mathrm{Current}\:\mathrm{in}\:\mathrm{smaller}\:\mathrm{loop}\:\mathrm{at}\:\mathrm{t}=\mathrm{0}\:\mathrm{is}\:\mathrm{0}. \\ $$$$\mathrm{and}\:\mathrm{there}\:\mathrm{is}\:\mathrm{also}\:\mathrm{no}\:\mathrm{battery}\:\mathrm{connected}\:\mathrm{to}\:\mathrm{larger}\:\mathrm{loop}\:\mathrm{then} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{source}\:\mathrm{of}\:\mathrm{current}\:\mathrm{in}\:\mathrm{larger}\:\mathrm{loop} \\ $$$$\mathrm{at}\:\mathrm{t}=\mathrm{0}\:? \\ $$
Commented by ajfour last updated on 23/Jul/18
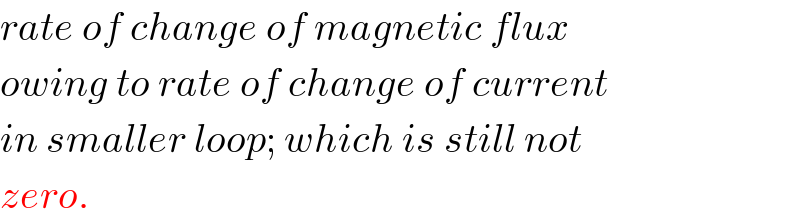
$${rate}\:{of}\:{change}\:{of}\:{magnetic}\:{flux} \\ $$$${owing}\:{to}\:{rate}\:{of}\:{change}\:{of}\:{current} \\ $$$${in}\:{smaller}\:{loop};\:{which}\:{is}\:{still}\:{not} \\ $$$${zero}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

