
Question Number 40505 by prof Abdo imad last updated on 23/Jul/18
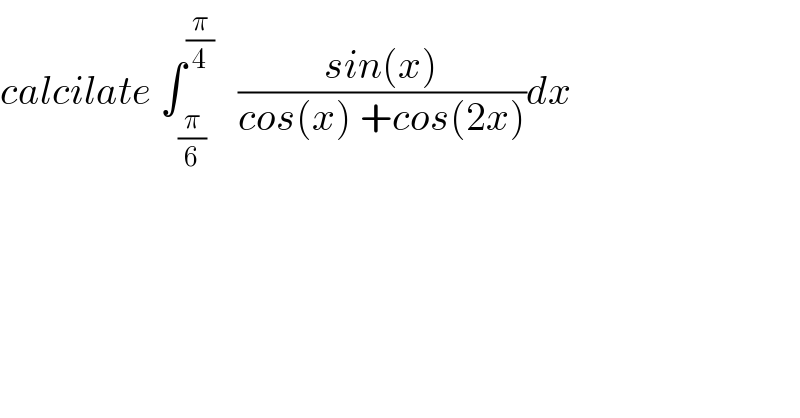
$${calcilate}\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)\:+{cos}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Answered by MJS last updated on 23/Jul/18
![cos 2x=2cos^2 x −1 ∫((sin x)/(2cos^2 x +cos x −1))dx= [t=cos x → dx=−(dt/(sin x))] =−∫(dt/(2t^2 +t−1))=−∫(dt/((2t−1)(t+1)))= =(1/3)∫(dt/(t+1))−(2/3)∫(dt/(2t−1))= =(1/3)ln(t+1)−(1/3)ln(2t−1)=(1/3)ln ((t+1)/(2t−1))= =(1/3)ln∣((cos x +1)/(2cos x −1))∣+C ∫_(π/6) ^(π/4) ((sin x)/(cos x +cos 2x))dx=(1/3)(ln ((4+3(√2))/2) −ln ((5+3(√3))/4))≈.160153](Q40518.png)
$$\mathrm{cos}\:\mathrm{2}{x}=\mathrm{2cos}^{\mathrm{2}} \:{x}\:−\mathrm{1} \\ $$$$\int\frac{\mathrm{sin}\:{x}}{\mathrm{2cos}^{\mathrm{2}} \:{x}\:+\mathrm{cos}\:{x}\:−\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:{x}\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:{x}}\right] \\ $$$$=−\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +{t}−\mathrm{1}}=−\int\frac{{dt}}{\left(\mathrm{2}{t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{\mathrm{2}{t}−\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left({t}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{2}{t}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\frac{{t}+\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\frac{\mathrm{cos}\:{x}\:+\mathrm{1}}{\mathrm{2cos}\:{x}\:−\mathrm{1}}\mid+{C} \\ $$$$\underset{\frac{\pi}{\mathrm{6}}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}\:+\mathrm{cos}\:\mathrm{2}{x}}{dx}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln}\:\frac{\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\mathrm{ln}\:\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\approx.\mathrm{160153} \\ $$
Commented by math khazana by abdo last updated on 23/Jul/18
$${thank}\:{you}\:{sir}\:{Mjs}. \\ $$
