
Question Number 404 by 123456 last updated on 30/Dec/14
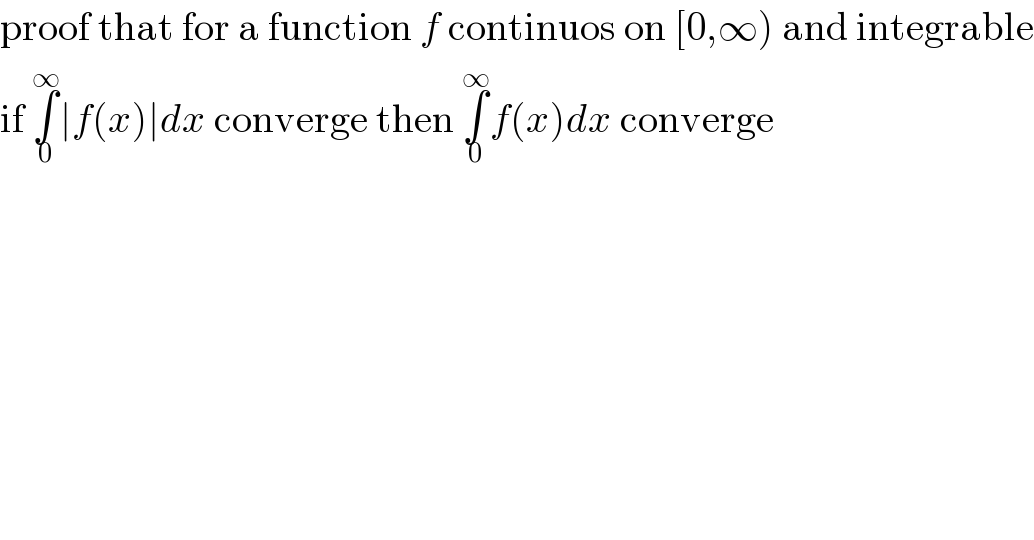
$$\mathrm{proof}\:\mathrm{that}\:\mathrm{for}\:\mathrm{a}\:\mathrm{function}\:{f}\:\mathrm{continuos}\:\mathrm{on}\:\left[\mathrm{0},\infty\right)\:\mathrm{and}\:\mathrm{integrable} \\ $$$$\mathrm{if}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\mid{f}\left({x}\right)\mid{dx}\:\mathrm{converge}\:\mathrm{then}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}{f}\left({x}\right){dx}\:\mathrm{converge} \\ $$
