
Question Number 40231 by Raj Singh last updated on 17/Jul/18
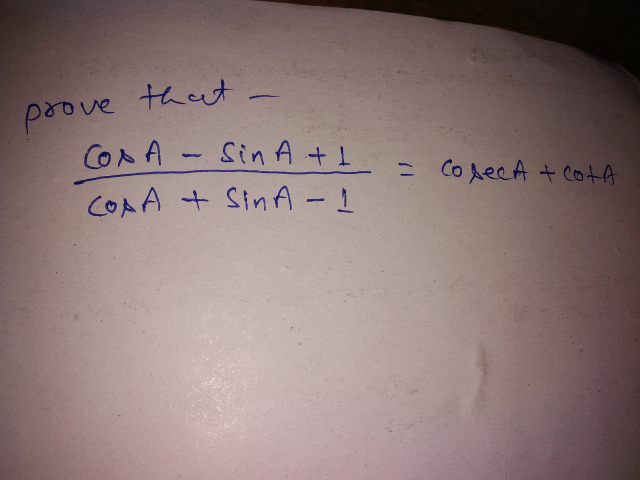
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jul/18
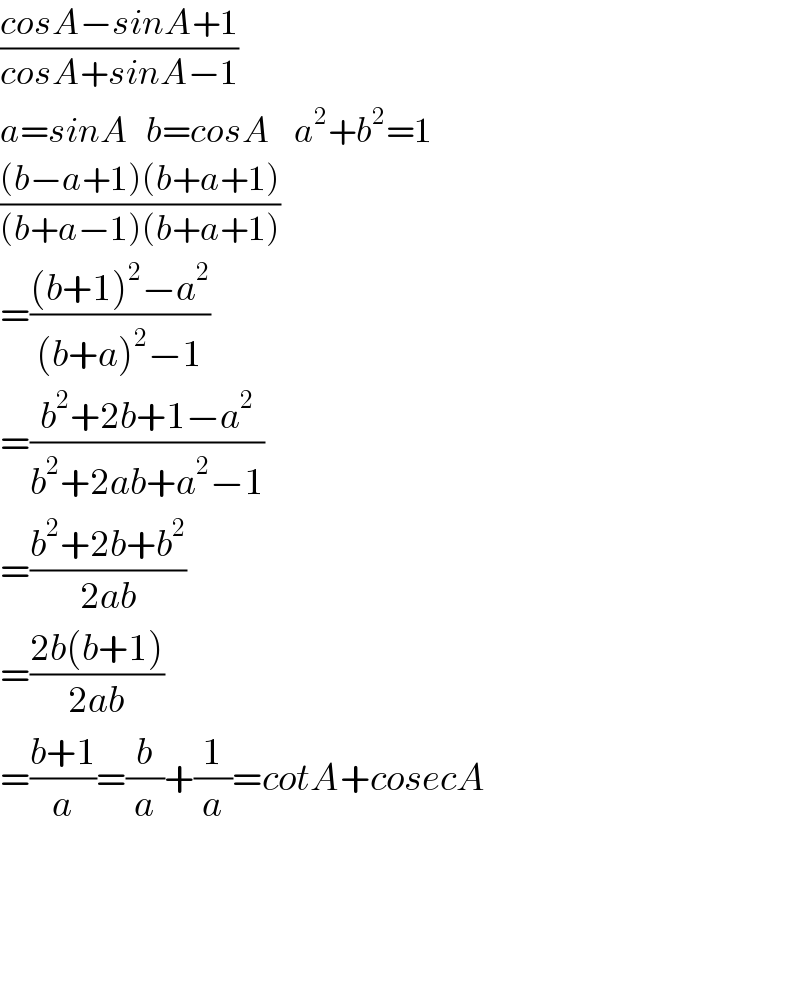
$$\frac{{cosA}−{sinA}+\mathrm{1}}{{cosA}+{sinA}−\mathrm{1}} \\ $$$${a}={sinA}\:\:\:{b}={cosA}\:\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{\left({b}−{a}+\mathrm{1}\right)\left({b}+{a}+\mathrm{1}\right)}{\left({b}+{a}−\mathrm{1}\right)\left({b}+{a}+\mathrm{1}\right)} \\ $$$$=\frac{\left({b}+\mathrm{1}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{\left({b}+{a}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}−{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{2}{ab}+{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{b}^{\mathrm{2}} +\mathrm{2}{b}+{b}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$=\frac{\mathrm{2}{b}\left({b}+\mathrm{1}\right)}{\mathrm{2}{ab}} \\ $$$$=\frac{{b}+\mathrm{1}}{{a}}=\frac{{b}}{{a}}+\frac{\mathrm{1}}{{a}}={cotA}+{cosecA} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Raj Singh last updated on 17/Jul/18

$${thank}\:{you} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jul/18

$${its}\:{ok}.... \\ $$
