
Question Number 40142 by maxmathsup by imad last updated on 16/Jul/18
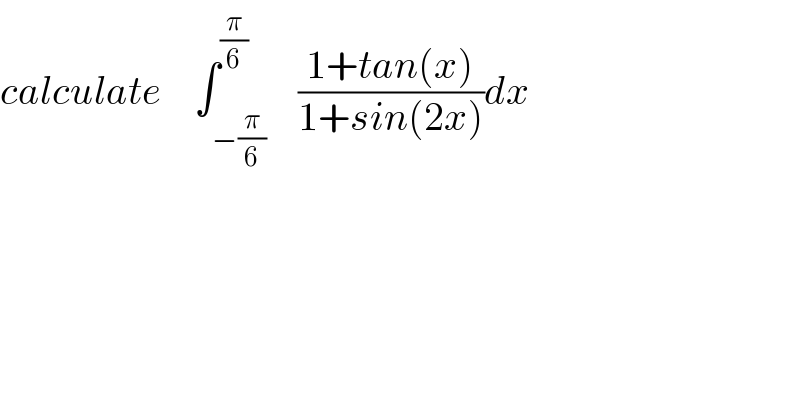
$${calculate}\:\:\:\:\int_{−\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} \:\:\:\frac{\mathrm{1}+{tan}\left({x}\right)}{\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 19/Jul/18
![let I = ∫_(−(π/6)) ^(π/6) ((1+tan(x))/(1+sin(2x)))dx changement tanx =t give I = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+((2t)/(1+t^2 )))) (dt/(1+t^2 )) = ∫_(−(1/(√3))) ^(1/(√3)) ((1+t)/(1+t^2 +2t)) dt = ∫_(−(1/(√3))) ^(1/(√3)) ((t+1)/((t+1)^2 ))dt = ∫_(−(1/(√3))) ^(1/(√3)) (dt/(t+1)) =[ln∣t+1∣]_(−(1/(√3))) ^(1/(√3)) =ln(1+(1/(√3)))−ln(1−(1/(√3)))=ln((√3)+1)−ln((√3)) −ln((√3)−1) +ln((√3)) I=ln((√3) +1) −ln((√3)−1)](Q40342.png)
$${let}\:\:{I}\:=\:\int_{−\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{\mathrm{1}+{tan}\left({x}\right)}{\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)}{dx}\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${I}\:=\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\frac{\mathrm{1}+{t}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\frac{\mathrm{1}+{t}}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:{dt} \\ $$$$=\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\frac{{t}+\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\:\frac{{dt}}{{t}+\mathrm{1}}\:=\left[{ln}\mid{t}+\mathrm{1}\mid\right]_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \\ $$$$={ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)−{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)={ln}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)−{ln}\left(\sqrt{\mathrm{3}}\right)\:−{ln}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:+{ln}\left(\sqrt{\mathrm{3}}\right) \\ $$$${I}={ln}\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)\:−{ln}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jul/18
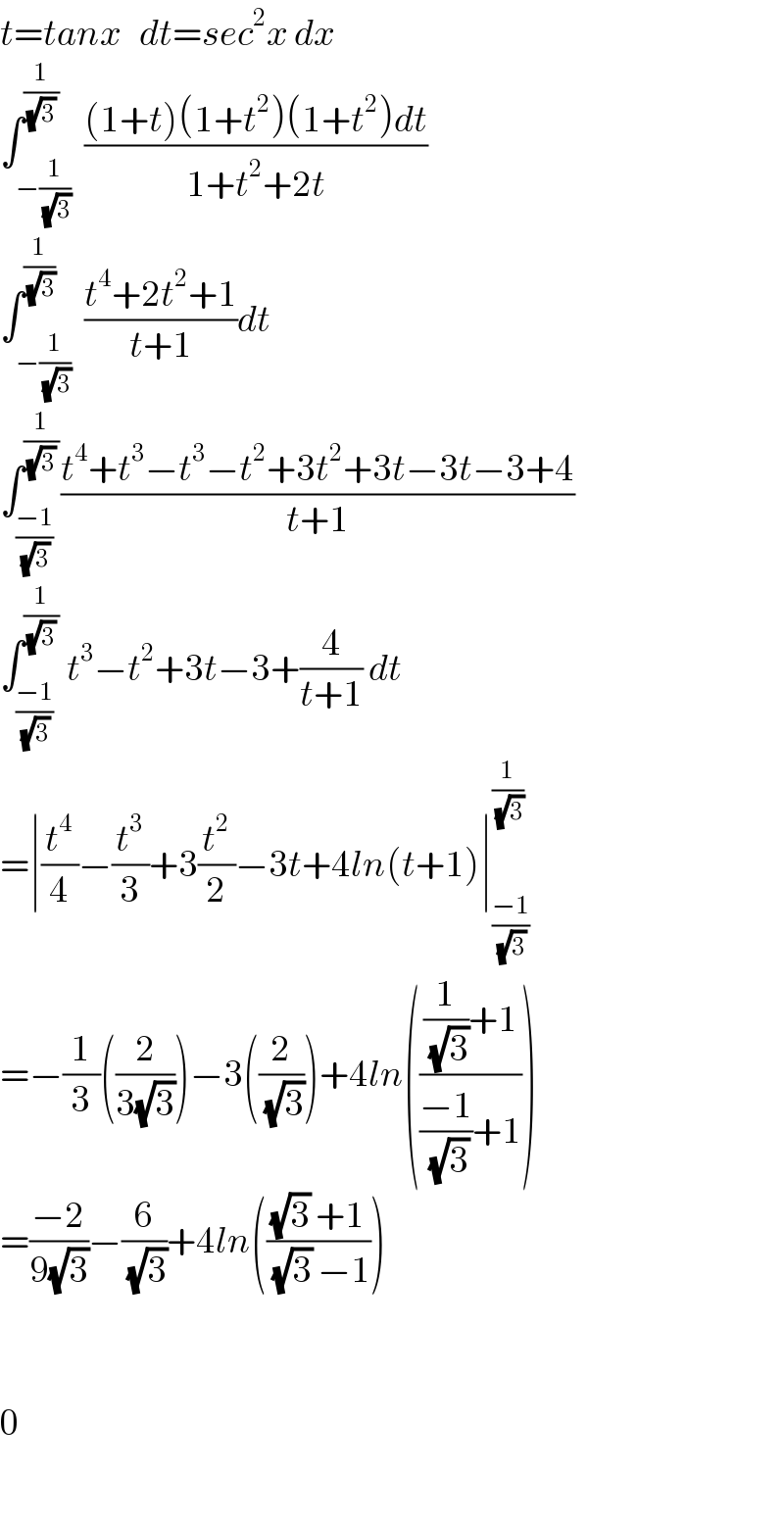
$${t}={tanx}\:\:\:{dt}={sec}^{\mathrm{2}} {x}\:{dx} \\ $$$$\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\:}} \:\frac{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}} \\ $$$$\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\frac{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{{t}+\mathrm{1}}{dt} \\ $$$$\int_{\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\:}} \frac{{t}^{\mathrm{4}} +{t}^{\mathrm{3}} −{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{3}{t}−\mathrm{3}+\mathrm{4}}{{t}+\mathrm{1}} \\ $$$$\int_{\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\:}} \:{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{3}+\frac{\mathrm{4}}{{t}+\mathrm{1}}\:{dt} \\ $$$$=\mid\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{3}\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{3}{t}+\mathrm{4}{ln}\left({t}+\mathrm{1}\right)\mid_{\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)−\mathrm{3}\left(\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)+\mathrm{4}{ln}\left(\frac{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\mathrm{1}}{\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}+\mathrm{1}}\right) \\ $$$$=\frac{−\mathrm{2}}{\mathrm{9}\sqrt{\mathrm{3}}}−\frac{\mathrm{6}}{\sqrt{\mathrm{3}}}+\mathrm{4}{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\mathrm{1}}{\sqrt{\mathrm{3}}\:−\mathrm{1}}\right) \\ $$$$ \\ $$$$ \\ $$$$\mathrm{0}\: \\ $$$$ \\ $$
