
Question Number 176893 by infinityaction last updated on 27/Sep/22
![[4(x^2 +2) +(9/((x^2 +2)))]_(min)](Q176893.png)
$$\:\:\:\:\left[\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\:+\frac{\mathrm{9}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)}\right]_{\mathrm{min}} \\ $$
Answered by mr W last updated on 27/Sep/22
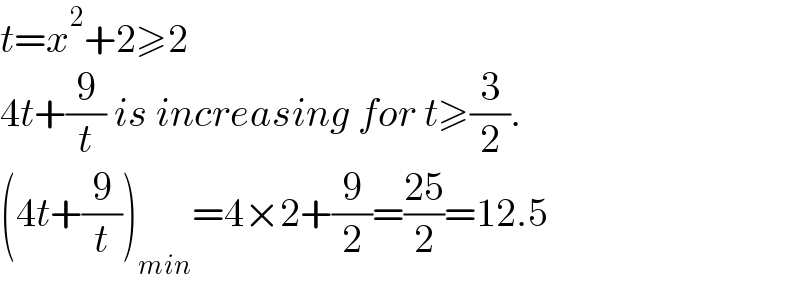
$${t}={x}^{\mathrm{2}} +\mathrm{2}\geqslant\mathrm{2} \\ $$$$\mathrm{4}{t}+\frac{\mathrm{9}}{{t}}\:{is}\:{increasing}\:{for}\:{t}\geqslant\frac{\mathrm{3}}{\mathrm{2}}. \\ $$$$\left(\mathrm{4}{t}+\frac{\mathrm{9}}{{t}}\right)_{{min}} =\mathrm{4}×\mathrm{2}+\frac{\mathrm{9}}{\mathrm{2}}=\frac{\mathrm{25}}{\mathrm{2}}=\mathrm{12}.\mathrm{5} \\ $$
