Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 207561 by hardmath last updated on 18/May/24

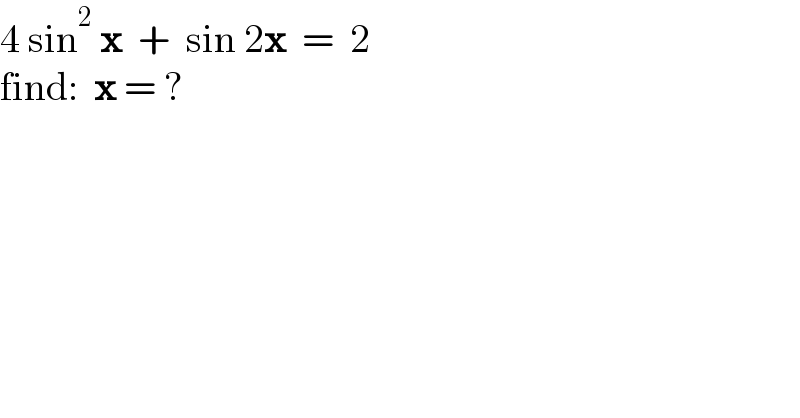
4 sin^2 x + sin 2x = 2 find: x = ?

$$\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\boldsymbol{\mathrm{x}}\:\:+\:\:\mathrm{sin}\:\mathrm{2}\boldsymbol{\mathrm{x}}\:\:=\:\:\mathrm{2} \\ $$$$\mathrm{find}:\:\:\boldsymbol{\mathrm{x}}\:=\:? \\ $$

Answered by mathzup last updated on 18/May/24

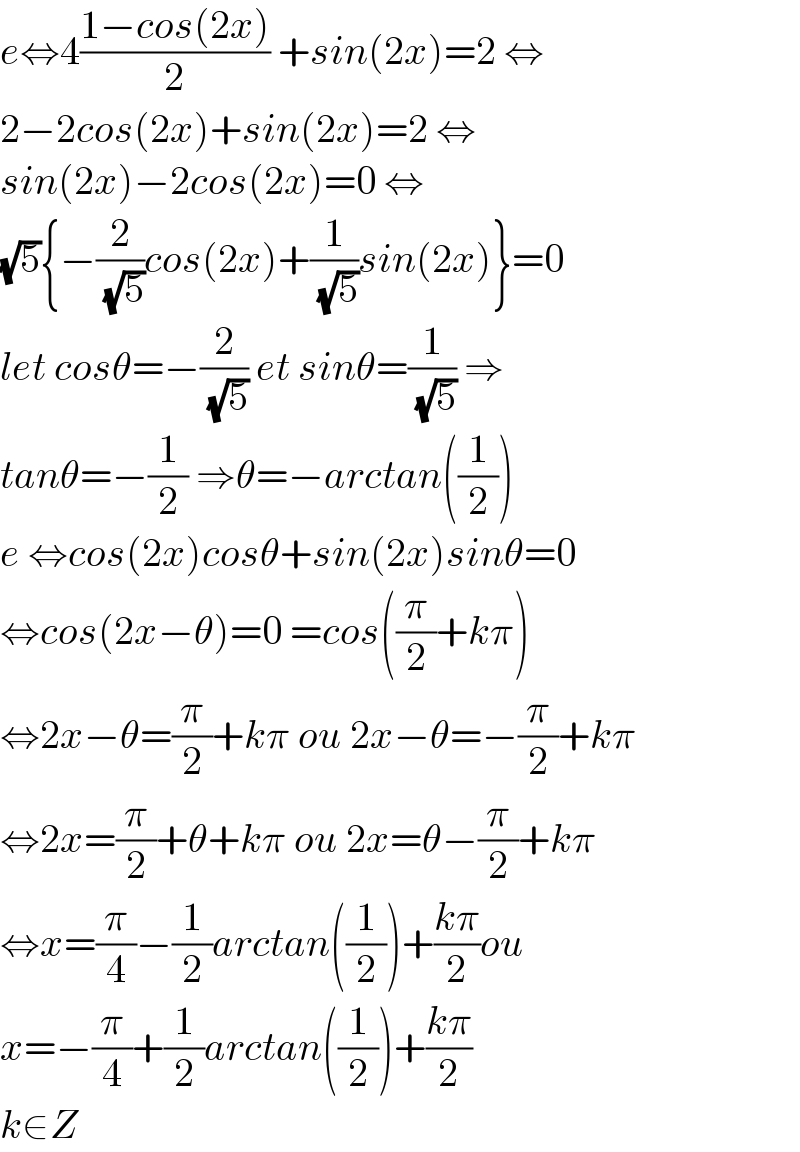
e⇔4((1−cos(2x))/2) +sin(2x)=2 ⇔ 2−2cos(2x)+sin(2x)=2 ⇔ sin(2x)−2cos(2x)=0 ⇔ (√5){−(2/( (√5)))cos(2x)+(1/( (√5)))sin(2x)}=0 let cosθ=−(2/( (√5))) et sinθ=(1/( (√5))) ⇒ tanθ=−(1/2) ⇒θ=−arctan((1/2)) e ⇔cos(2x)cosθ+sin(2x)sinθ=0 ⇔cos(2x−θ)=0 =cos((π/2)+kπ) ⇔2x−θ=(π/2)+kπ ou 2x−θ=−(π/2)+kπ ⇔2x=(π/2)+θ+kπ ou 2x=θ−(π/2)+kπ ⇔x=(π/4)−(1/2)arctan((1/2))+((kπ)/2)ou x=−(π/4)+(1/2)arctan((1/2))+((kπ)/2) k∈Z

$${e}\Leftrightarrow\mathrm{4}\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:+{sin}\left(\mathrm{2}{x}\right)=\mathrm{2}\:\Leftrightarrow \\ $$$$\mathrm{2}−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{2}{x}\right)=\mathrm{2}\:\Leftrightarrow \\ $$$${sin}\left(\mathrm{2}{x}\right)−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)=\mathrm{0}\:\Leftrightarrow \\ $$$$\sqrt{\mathrm{5}}\left\{−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}{cos}\left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{sin}\left(\mathrm{2}{x}\right)\right\}=\mathrm{0} \\ $$$${let}\:{cos}\theta=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:{et}\:{sin}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\Rightarrow \\ $$$${tan}\theta=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\theta=−{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${e}\:\Leftrightarrow{cos}\left(\mathrm{2}{x}\right){cos}\theta+{sin}\left(\mathrm{2}{x}\right){sin}\theta=\mathrm{0} \\ $$$$\Leftrightarrow{cos}\left(\mathrm{2}{x}−\theta\right)=\mathrm{0}\:={cos}\left(\frac{\pi}{\mathrm{2}}+{k}\pi\right) \\ $$$$\Leftrightarrow\mathrm{2}{x}−\theta=\frac{\pi}{\mathrm{2}}+{k}\pi\:{ou}\:\mathrm{2}{x}−\theta=−\frac{\pi}{\mathrm{2}}+{k}\pi \\ $$$$\Leftrightarrow\mathrm{2}{x}=\frac{\pi}{\mathrm{2}}+\theta+{k}\pi\:{ou}\:\mathrm{2}{x}=\theta−\frac{\pi}{\mathrm{2}}+{k}\pi \\ $$$$\Leftrightarrow{x}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{k}\pi}{\mathrm{2}}{ou} \\ $$$${x}=−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{k}\pi}{\mathrm{2}} \\ $$$${k}\in{Z} \\ $$

Commented by hardmath last updated on 19/May/24

thank you very much

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com